
解析函数
解 析 函 数

第七讲 初等函数之三角函数
第七讲 初等函数之三角函数

初等函数 1.三角函数 定义1:对于任意复数z=x+iy,函数sinz= eiz-e-iz 2i 分别称为复变量z的正弦函数和余弦函数: COSZ Sinz etz-e-iz i(el-e-)l(e-tz-elr) 2i 2 2 COS(z+2=lt2n+e-iG+2)ezte- 2 2 sinz,c0sz都是单值函数和周期函数
初等函数 1.三角函数 定义1:对于任意复数𝒛 = 𝒙 + 𝒊𝒚,函数𝒔𝒊𝒏𝒛 = 𝒆 𝒊𝒛−𝒆 −𝒊𝒛 𝟐𝒊 , 𝒄𝒐𝒔𝒛 = 𝒆 𝒊𝒛+𝒆 −𝒊𝒛 𝟐 ,分别称为复变量𝒛的正弦函数和余弦函数。 s𝒊𝒏𝒛, 𝒄𝒐𝒔𝒛都是单值函数和周期函数。 𝒔𝒊𝒏𝒛 = 𝒆 𝒊𝒛−𝒆 −𝒊𝒛 𝟐𝒊 = −𝒊(𝒆 𝒊𝒛−𝒆 −𝒊𝒛) 𝟐 = 𝒊(𝒆 −𝒊𝒛−𝒆 𝒊𝒛) 𝟐 𝒄𝒐𝒔(𝒛 + 𝟐𝝅) = 𝒆 𝒊(𝒛+𝟐𝝅)+𝒆 −𝒊(𝒛+𝟐𝝅) 𝟐 = 𝒆 𝒊𝒛+𝒆 −𝒊𝒛 𝟐

三角函数的性质 (1)运算法则:sin2z+c0s2z=1 c0s(z1±z2)=c0Sz1c0sz2干sinz1sinz2, sin(z1±z2)=sinz1c0sz2±c0Sz1Sinz2, (2)奇偶性:sinz奇函数,cosz偶函数; (3)解析性:在复平面上处处解析 (cosz)'=-sinz ,(sinz)'=cosz (4)无界性在复平面上无界。 例cosy=7无界,y)
三角函数的性质 (1)运算法则: cos 𝒛𝟏 ± 𝒛𝟐 = 𝒄𝒐𝒔𝒛𝟏𝒄𝒐𝒔𝒛𝟐 ∓ 𝒔𝒊𝒏𝒛𝟏𝒔𝒊𝒏𝒛𝟐, s𝒊𝒏 𝒛𝟏 ± 𝒛𝟐 = 𝒔𝒊𝒏𝒛𝟏𝒄𝒐𝒔𝒛𝟐 ± 𝒄𝒐𝒔𝒛𝟏𝒔𝒊𝒏𝒛𝟐, s𝒊𝒏 𝟐𝒛 + 𝒄𝒐𝒔 𝟐𝒛 = 𝟏 (2)奇偶性: 𝒔𝒊𝒏𝒛 奇函数,cosz 偶函数; (3)解析性:在复平面上处处解析 (𝒄𝒐𝒔𝒛)ˊ = −𝒔𝒊𝒏𝒛 , (𝒔𝒊𝒏𝒛)ˊ = 𝒄𝒐𝒔𝒛 (4)无界性:在复平面上无界。 例cos 𝒊𝒚 = e −y+e y 2 无界, (𝒚 → ∞)
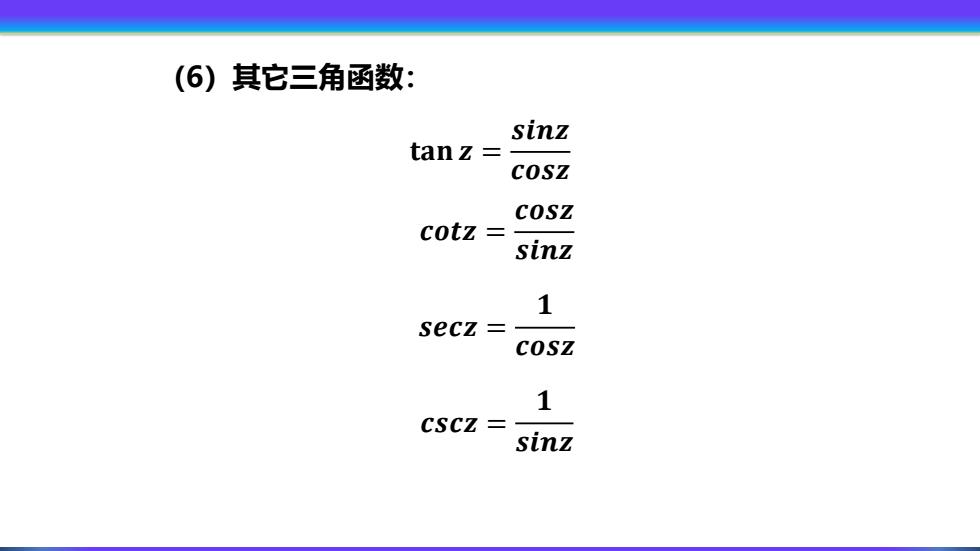
(6)其它三角函数: sinz tanz= COSZ COSZ cotz= sinz 1 secz 1 CSCZ= sinz
(6)其它三角函数: 𝐭𝐚𝐧 𝒛 = 𝒔𝒊𝒏𝒛 𝒄𝒐𝒔𝒛 𝒄𝒐𝒕𝒛 = 𝒄𝒐𝒔𝒛 𝒔𝒊𝒏𝒛 𝒔𝒆𝒄𝒛 = 𝟏 𝒄𝒐𝒔𝒛 𝒄𝒔𝒄𝒛 = 𝟏 𝒔𝒊𝒏𝒛