
留数及其应用
留数及其应用

第五讲 留数的应用
第五讲 留数的应用
留数及其应用 1.留数定理 定理2:设函数f(z)在区域D内除有限个孤立奇点 z1,z2,2n外处处解析,C是D内包围各奇点的一 条正向简单闭曲线,则 D ∮cfad n =2πi Res [f(z),zk] C
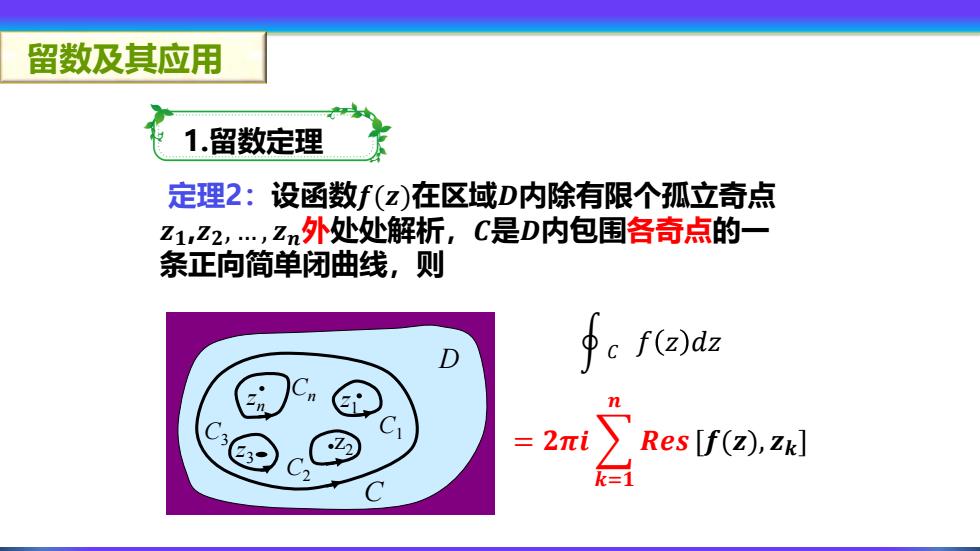
留数及其应用 1.留数定理 定理2:设函数𝒇(𝒛)在区域𝑫内除有限个孤立奇点 𝒛𝟏,𝒛𝟐, . , 𝒛𝒏外处处解析,𝑪是𝑫内包围各奇点的一 条正向简单闭曲线,则 ර 𝐶 𝑓 𝑧 𝑑𝑧 = 𝟐𝝅𝒊 𝒌=𝟏 𝒏 𝑹𝒆𝒔 [𝒇(𝒛), 𝒛𝒌] D z1 z z 2 3 zn C1 C2 C3 Cn C

2.留数的应用: 例1:计算积分∮4-22品z. 5z-2 解:·z=0是f(z)的一阶极点, Res(f().0)-2 5z-2 :z=1是f(z)的二阶极点, Res((z.)1)=2=m(5-=2 2高1 A1=2ze-1zdz=2πi(-2+2)=0 5z-2
2.留数的应用: 例1:计算积分ׯ| 𝒛| = 𝟐 𝟓𝒛−𝟐 𝒛(𝒛−𝟏) 𝟐dz. 解: ∵ z = 0是𝑓 𝑧 的一阶极点, 𝑹𝒆𝒔 𝒇 𝒛 , 𝟎 = ฬ 𝟓𝒛−𝟐 (𝒛−𝟏) 𝟐+𝟐𝒛(𝒛−𝟏) 𝒛=𝟎 = −𝟐 ∵ z = 1是𝑓 𝑧 的二阶极点, 𝑹𝒆𝒔 𝒇(𝒛), 𝟏 = 𝐥𝐢𝐦 𝒛→𝟏 𝒅 𝒅𝒛 𝟓𝒛−𝟐 𝒛 = 𝐥𝐢𝐦 𝒛→𝟏 (𝟓 − 𝟐 𝒛 )′ = 𝟐 | ׯ 𝒛| = 𝟐 𝟓𝒛−𝟐 𝒛(𝒛−𝟏) 𝟐 𝒅𝒛=2𝝅𝒊 −𝟐 + 𝟐 = 𝟎

例2:计算积分∮4=2 G-Ddz. sin2z 举例 解:·z=1是f(z)的一阶极点, Res0fa,1)=41 sin2z sin21 'z=0是f(z)的可去极点, sin-z Res(f(z),0)=lim =0 0(2-1)z dz 2nl(sin)=2misin2
举例 例2:计算积分ׯ| 𝒛| = 𝟐 𝒔𝒊𝒏𝟐𝒛 𝒛−𝟏 𝒛 𝟐 𝒅𝒛. 解: ∵ 𝒛 = 𝟏是𝒇 𝒛 的一阶极点, 𝑹𝒆𝒔 𝒇 𝒛 , 𝟏 = ฬ 𝒔𝒊𝒏𝟐𝒛 𝒛 𝟐+𝟐𝒛(𝒛−𝟏) 𝒛=𝟏 = 𝒔𝒊𝒏𝟐𝟏 ∵ 𝒛 = 𝟎是𝒇 𝒛 的可去极点, 𝑹𝒆𝒔 𝒇(𝒛), 𝟎 = 𝐥𝐢𝐦 𝒛→𝟎 𝒔𝒊𝒏𝟐𝒛 𝒛 − 𝟏 𝒛 = 𝟎 |ׯ 𝒛| = 𝟐 𝒔𝒊𝒏𝟐𝒛 𝒛−𝟏 𝒛 𝟐 𝒅𝒛 =2𝝅𝒊 𝒔𝒊𝒏𝟐𝟏 + 𝟎 = 𝟐𝝅𝒊𝒔𝒊𝒏𝟐𝟏