
傅里叶变换
傅里叶变换

第三讲 单位中激数
第三讲 单位冲激函数

单位冲激函数 傅里叶级数与傅里叶变换以不同形式反映了周期函数与 非周期函数的频谱特性,是否能够将离散频谱以连续频 谱的方式表现出来? 这就需要引进单位冲激函数与广义傅氏变换。 在工程实际问题中,有许多物理现象具有一种脉冲 特征,他们在某一瞬间或某一点出现,如瞬时冲击 力、脉冲电流、质点质量等等,这些物理量均不能 用通常函数形式去描述
单位冲激函数 傅里叶级数与傅里叶变换以不同形式反映了周期函数与 非周期函数的频谱特性,是否能够将离散频谱以连续频 谱的方式表现出来? 在工程实际问题中,有许多物理现象具有一种脉冲 特征,他们在某一瞬间或某一点出现,如瞬时冲击 力、脉冲电流、质点质量等等,这些物理量均不能 用通常函数形式去描述。 这就需要引进单位冲激函数与广义傅氏变换

1.单位冲激函数引入 引例:设有长度为的均匀细杆放在x轴的0,]上,其质量为m, 用pe(x)表示它的线密度,则有 m 0≤x≤e Pε(x) 0, 其他 当e一0时,p(G)=lpe()={ ,X=0 0 0,x≠0 且 p(x)dx m, 满足这两个条件的函数称为单位 冲激函数(δ函数狄拉克函数)
1.单位冲激函数引入 引例:设有长度为𝜺的均匀细杆放在𝒙轴的[𝟎,𝜺]上,其质量为𝒎, 用𝝆𝜺 (𝒙)表示它的线密度,则有 当𝜺→0时, 且 𝝆𝜺 𝒙 = ቐ 𝒎 𝜺 , 𝟎 ≤ 𝒙 ≤ 𝜺 𝟎, 其他 . 𝝆 𝒙 = 𝐥𝐢𝐦 𝜺→𝟎 𝝆𝜺 𝒙 = ቊ ∞, 𝒙 = 𝟎 𝟎, 𝒙 ≠ 𝟎 න −∞ +∞ 𝝆 𝒙 𝒅𝒙 = 𝒎 , 满足这两个条件的函数称为单位 冲激函数(𝜹函数\狄拉克函数)
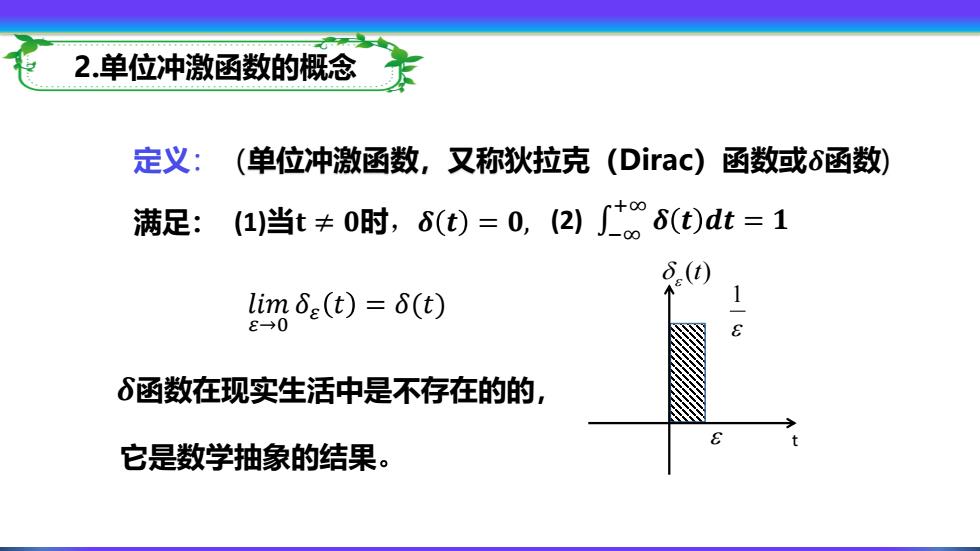
2.单位冲激函数的概念 定义:(单位冲激函数,又称狄拉克 (Dirac)函数或函数) 满足:(1)当t≠0时,6(t)=0,(2)∫6(t)dt=1 6(t) limδe(t)=6(t) E→0 δ函数在现实生活中是不存在的的, 它是数学抽象的结果
2.单位冲激函数的概念 定义:(单位冲激函数,又称狄拉克(Dirac)函数或𝜹函数) 满足: (1)当𝐭 ≠ 𝟎时,𝜹 𝒕 = 𝟎, (2) ∞− +∞ 𝜹 𝒕 𝒅𝒕 = 𝟏 1 (t) t 𝑙𝑖𝑚 𝜀→0 𝛿𝜀 𝑡 = 𝛿(𝑡) 𝜹函数在现实生活中是不存在的的, 它是数学抽象的结果