
拉普拉斯变换
拉普拉斯变换

第二讲 拉普拉斯变换的性质
第二讲 拉普拉斯变换的性质

化1拉普拉斯变换的性质东 1、线性性质: 设F(s)=c[f(t)],G(s)=E[g(t)],a,B为常数,则 C[af(t)+Bg(t)]=aF(s)+BG(s) C-1[aF(s)+BG(s)]=af(t)+Bg(t)
1.拉普拉斯变换的性质 1、线性性质:
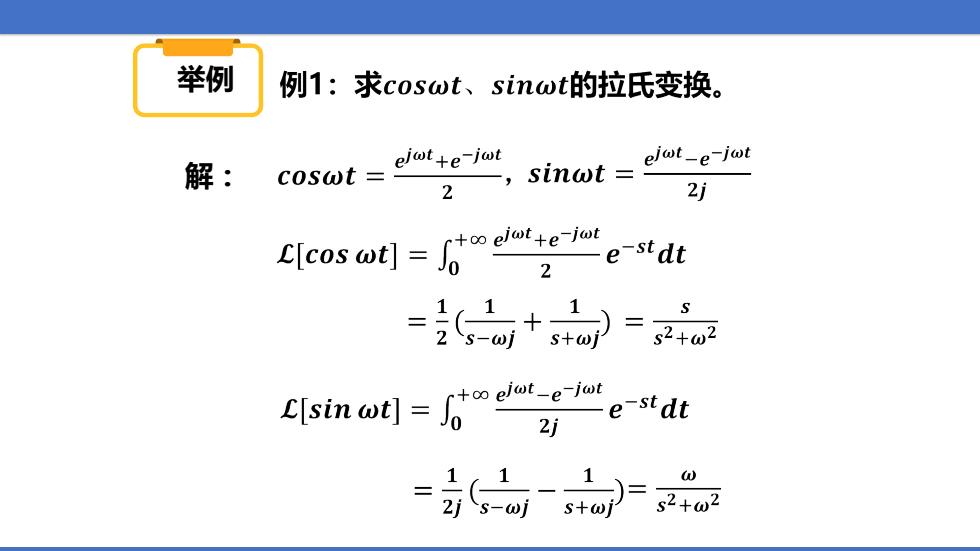
举例 例1:求coswt、sinwt的拉氏变换。 解: COSWt=olut+e-jwt 2 sinat =elot-e-lot 2j teos t =+)=4o csnw-"m2。etar -1)= S+ωj s2+w2
举例 解:

基础练习 1.求下列函数的拉氏变换F(s)。 S (1)f(t)=as 4t 解:[cos4t]= 52+16 3 (2)ft)=in3t 解:c[sin3U=s2+9 2 3s (3)f(d)=2sint+3c0s2t解:Cf(t]=32+1+s2+4
基础练习 (ᵼ )ᵈ(ᵉ) = ᵈᵉᵉ ᵽ ᵉ (ᵽ )ᵈ(ᵉ) = ᵉᵈᵈ ᵽ ᵉ 解: 解: 解: