
复数与复变函数
复数与复变函数

第八讲 复变函数的极限与连续
第八讲 复变函数的极限与连续
复变函数的极限与连续 转1.复变函数的极限 定义1:设函数w=f(z),在z0的去心邻域内0<|z-2ol<p 有定义,若有确定的复数A(A≠o∞)存在,对任意给定ε>0,总 存在一个正数6,对于满足0<|z-zol<6(0<6≤p)的一切z, 都有f(z)-A<ε,则称A为f(z)当z→Zo时的极限,记作: lim f(z)=A Z→Z0 f(z)→A
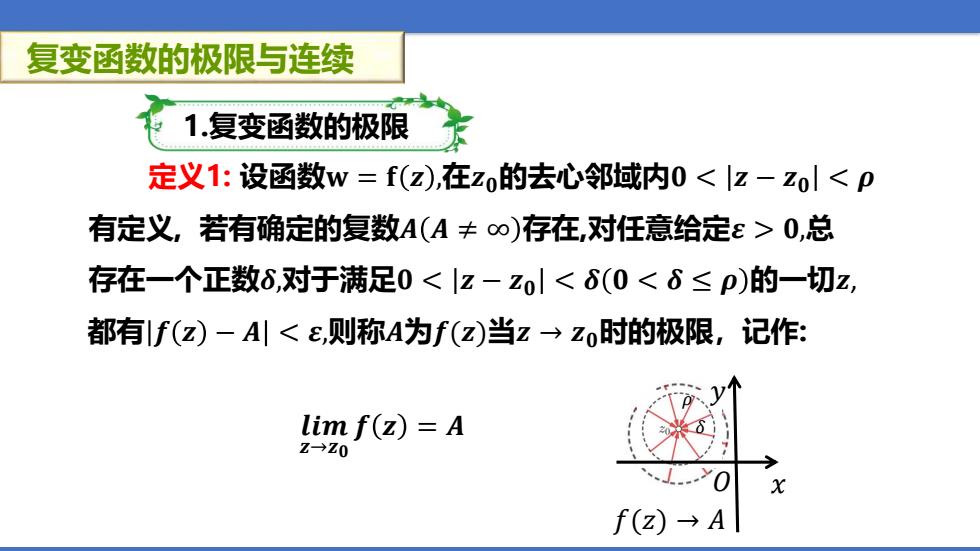
复变函数的极限与连续 1.复变函数的极限 都有 𝒇 𝒛 − 𝑨 < 𝜺,则称𝑨为𝒇(𝒛)当𝒛 → 𝒛𝟎时的极限,记作: 𝑂 𝑥 𝒍𝒊𝒎 𝒛→𝒛𝟎 𝒇 𝒛 = 𝑨 𝑓(𝑧) → 𝐴 定义1: 设函数𝐰 = 𝐟 𝒛 ,在𝒛𝟎的去心邻域内𝟎 < 𝒛 − 𝒛𝟎 < 𝝆 有定义, 𝜌 𝑦 𝛿 若有确定的复数𝑨 𝑨 ≠ ∞ 存在,对任意给定𝜺 > 𝟎,总 存在一个正数𝜹,对于满足𝟎 < 𝒛 − 𝒛𝟎 < 𝜹 𝟎 < 𝜹 ≤ 𝝆 的一切𝒛

2.复变函数极限的几何意义 w f(z) X 0 Z→Z0 f(z)→A 说明:z以任意方式趋近于20,但不论怎样趋近, f(z)的值总趋近于A
2.复变函数极限的几何意义 𝑂 𝑥 𝑦 𝛿 𝑂 𝑢 𝑤 = 𝑓(𝑧) v 𝜀 说明:𝒛以任意方式趋近于𝒛𝟎,但不论怎样趋近, 𝒇(𝒛)的值总趋近于𝑨。 𝑧 → 𝑧0 𝑓(𝑧) → 𝐴

2.复变函数的极限的四则运算法测 设limf(z)=A,limg(z)=B, Z→Z0 Z→Z0 则lim[f(z)±g(z)]=A±B; →Z0 lim[f(z)g(z)]=AB; Z→Z0 f(z)A 0g(②=B(B≠0), lim
2.复变函数的极限的四则运算法则 设𝒍𝒊𝒎 𝒛→𝒛𝟎 𝒇 𝒛 = 𝑨,𝒍𝒊𝒎 𝒛→𝒛𝟎 𝒈 𝒛 = 𝑩, 则𝒍𝒊𝒎 𝒛→𝒛𝟎 𝒇 𝒛 ± 𝒈 𝒛 = 𝑨 ± 𝑩; 𝒍𝒊𝒎 𝒛→𝒛𝟎 [𝒇 𝒛 𝒈 𝒛 ] = 𝑨𝑩; 𝒍𝒊𝒎 𝒛→𝒛𝟎 𝒇 𝒛 𝒈 𝒛 = 𝑨 𝑩 𝑩 ≠ 𝟎