
第四讲 傅里叶级数的计算
无 穷 级 数 第四讲 傅里叶级数的计算
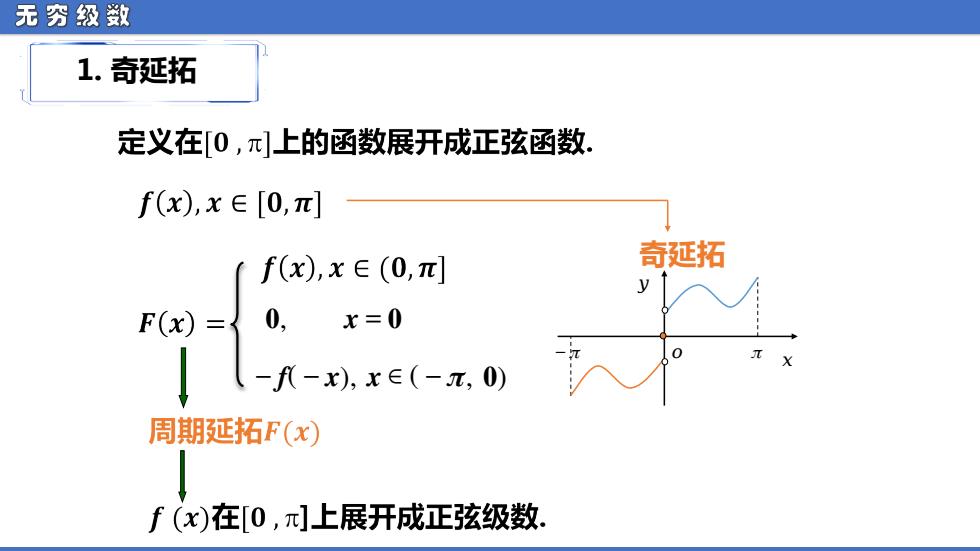
无穷级数 1.奇延拓 定义在[0,π上的函数展开成正弦函数 f(x),x∈[0,π] ff(x),x∈(0,π] 奇延拓 F()= 0, x=0 1-x-x0 周期延拓F(x) f(x)在[0,]上展开成正弦级数
无 穷 级 数 1. 奇延拓 奇延拓 ᵆ ᵅ ᵰ ᵆ − ᵰ ᵼ , ᵉ = ᵼ − ᵈ( − ᵉ ), ᵉ ∈ ( − ᵴ , ᵼ )
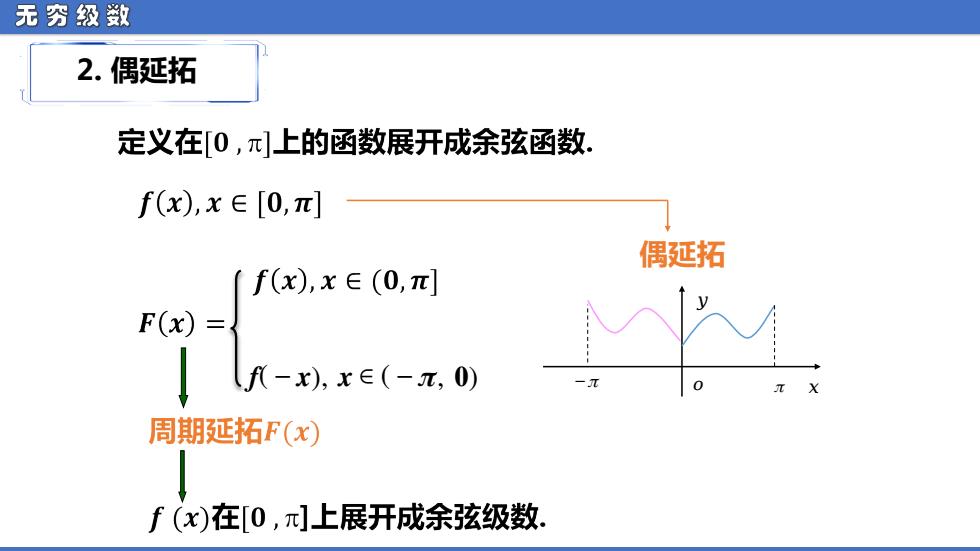
无穷级数 2.偶延拓 定义在[0,π]上的函数展开成余弦函数 f(x),x∈[0,π] 偶延拓 (f(x),x∈(0,π] F(x)= -,xe-x0 周期延拓F(x) f(x)在[0,上展开成余弦级数
无 穷 级 数 2. 偶延拓 偶延拓 ᵈ( − ᵉ ), ᵉ ∈ ( − ᵴ , ᵼ ) − ᵰ ᵅ ᵰ ᵆ ᵆ

无穷级数 举例 例1:将函数f(x)=x+1,x∈[0,π]分别展开成 余弦与正弦级数, 解:先求正弦级数.去掉端点,将f(x)作奇周期延拓, nf)sinnxdx +1)sinnxdx xcosnx sinnx cognx n n =2(1-πcosnm-cosnπ) nπ
无 穷 级 数 举例 1 ᵰ ᵆ ᵆ ᵅ 解: 先求正弦级数.去掉端点, 将 f (x) 作奇周期延拓, − ᵰ

无穷级数 bn=2[1-(-1)"π-(-1)n则 nπ 2 π+2 π 2k-1'n=2k-1 (k=1,2,. n=2k 因此得 x+1=引π+2)smx-受sn2+" 3 sin3x π sin4x+.](0<x<m) 注意:在端点x= 0,π,级数的和为0,与给定函数 f(x)=x+1的值不同
无 穷 级 数 = ᵈ = ᵽ ᵈ − ᵼ (ᵈ = ᵼ , ᵽ , ⋯ ) (ᵼ < ᵉ < ᵴ ) 因此得 注意: 与给定函数 1 ᵰ ᵆ ᵆ − ᵰ ᵅ