
第六讲 绝对收敛与条件收敛
无 穷 级 数 第六讲 绝对收敛与条件收敛

无穷级敛 1.绝对收敛与条件收敛 00 00 定义对任意项级数) 山n,若〉,|un收敛,则称原级数绝对收敛 n=1 n=1 若原级数收敛,但取绝对值以后的级数发散,则称原级数条件收敛 例如: 1 1- 绝对收敛 1 34++(-1)-11+. 1 1 条件收敛 m
无 穷 级 数 1.绝对收敛与条件收敛 定义.对任意项级数 例如: 绝对收敛 条件收敛

无穷级数 定理1绝对收敛的级数一定收敛, 00 证:设)un收敛,令pn=(un+lunl)n=1,2.) n=1 解得:un=2vn-unl)(n=1,2,.) :un≥0,且un≤un÷∑”n收敛 m=1 X● :∑2n收敛∑4nl收敛,∑ un收敛 1 m=1 n=1
无 穷 级 数 定理1.绝对收敛的级数一定收敛. 证:
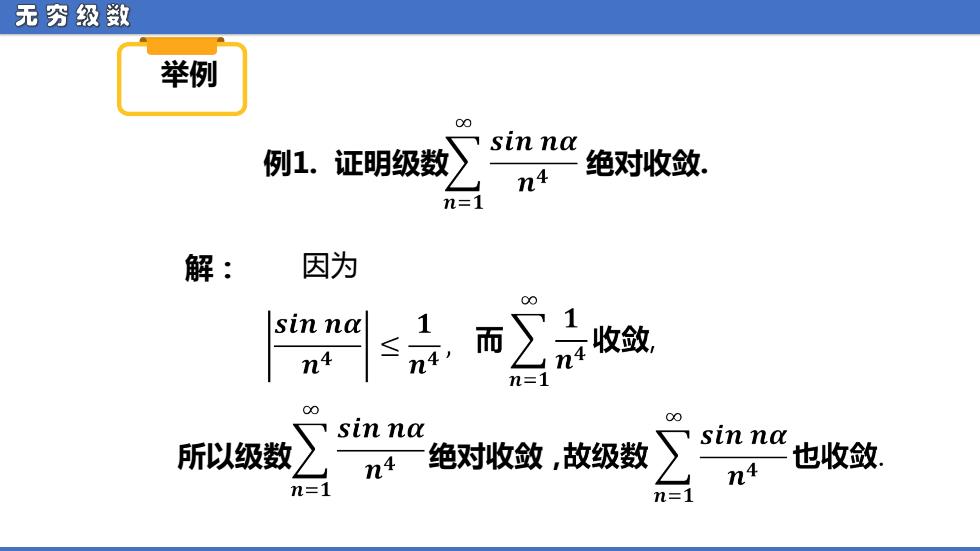
无穷级数 举例 00 sin na 例1.证明级数 24 绝对收敛 n=1 解: 因为 叫=是而是收效 m=1 00 sin na sin na 所以级数 n4 绝对收敛故级数 也收敛: n=1 n4
无 穷 级 数 举例 例1. 证明级数 绝对收敛. 解: 所以级数 绝对收敛, 因为
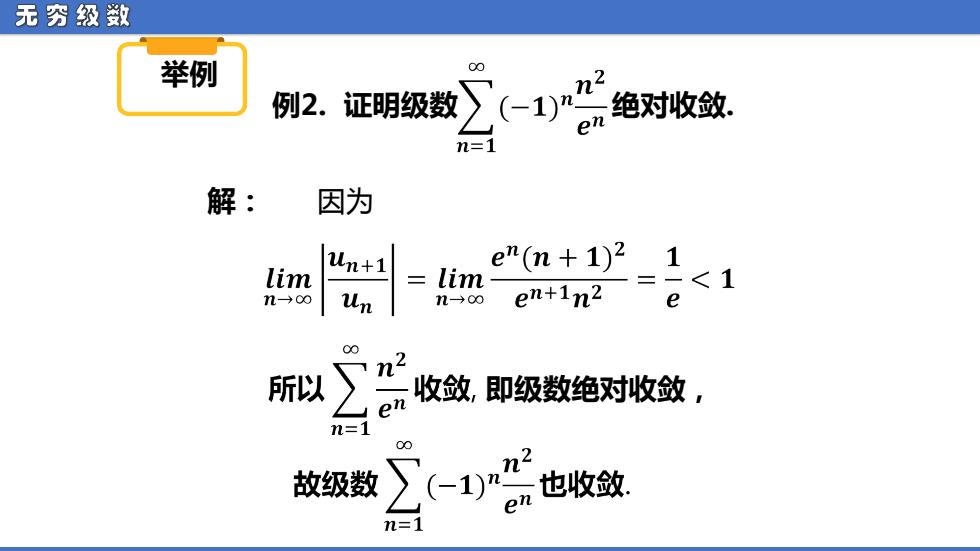
无穷级数 举例 00 例2. 证明级数》-不 绝对收敛 n=1 解: 因为 lim n+1 lim e"(n+1)21 n→o∞ Un n→oo en+in2 二<1 e 00 所以 en 收敛,即级数绝对收敛, n=1 00 故级数 也收蚊 ∑( n=1
无 穷 级 数 举例 例2. 证明级数 绝对收敛. 解: 即级数绝对收敛, 因为