
第三讲 傅里叶级数的计算
无 穷 级 数 第三讲 傅里叶级数的计算
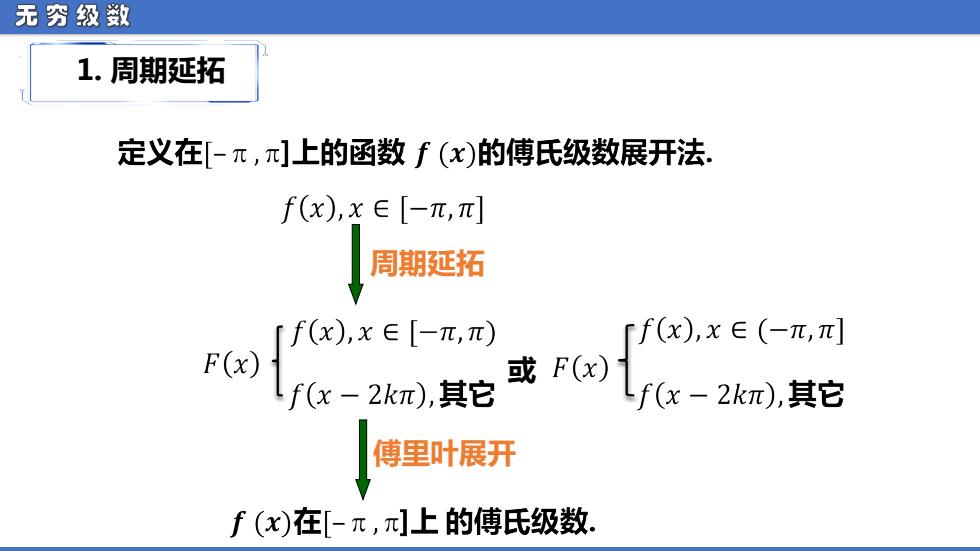
无穷级数 1.周期延拓 定义在[-元,π]上的函数f(x)的傅氏级数展开法 f(x),x∈[-π,π] 周期延拓 「f(x),x∈[-π,π) 「f(x),x∈(-π,π] F(x) c-2km, 或F(x) Lf(x-2kπ),其它 傅里叶展开 f(x)在[-π,π]上的傅氏级数
无 穷 级 数 1. 周期延拓 周期延拓 或 傅里叶展开

无穷级数 举例 ∫-x,-π≤x<0展成傅里叶级数, 例1:将函数f(,=x0≤x<π 解:将f(x)延拓成以2π为周期的函数F(x),则 a=是」nf()dx=是xdx-是」nxdx=元 an=是∫nfx)cosnxdx =是0 xcosnxdx-是∫.xcosnxdx
无 穷 级 数 举例 ᵰ ᵰ ᵆ ᵆ

无穷级数 r xdsinnx nπJ oxdsinnx-1 o nπJ-办 xsinnx6+.cosnx6-高cosnx nn 1=n=2k-1 kEz. n2π 0,n=2k bn=∫nf(x)sinnxdx =是xsinnxdx-是∫0 xsinnxdx xcosnxxcosnx =0
无 穷 级 数 = ᵼ

无穷级数 -4 f(x)= 2+ 2n-1)2元cos(2n-1)x,(xe[-m,m) 取x=0级数收敛于0,则有 1 111 、 2m+=1+京京+京+ 8 2 00 、>2三1× 11 22 1 32 而+ =o解得o= 8 6 00 (-1)n+1 111 π2π2π2 2 一1 22十32-42+.= 82412 =1
无 穷 级 数