
复数的概念与计算
复数的概念与计算

第五讲 复数乘方与开方 复球面
第五讲 复数乘方与开方 复球面

1.复数的乘方与开方 (1)乘方zn=z.z=rn(cosn0+isinn0) n (2)开方 设w1=z,则称w是z的n次方根。记为wW=点 √2表示z的n次方根的主值。 方根的计算公式 设z=r(cos0+isin0),则 w=点=r( 0+2kπ 0+2kπ k∈Z
1.复数的乘方与开方 (1) 乘方 𝒛 𝒏 = 𝒛 ⋯ 𝒛 𝒏 = 𝒓 𝒏 (𝒄𝒐𝒔 𝒏𝜽 + 𝒊𝒔𝒊𝒏 𝒏𝜽) (2) 开方 设𝒘𝒏 = 𝒛,则称𝒘是𝒛的𝒏次方根。记为𝒘 = 𝒛 𝟏 𝒏 , 𝒛 𝒏 表示𝒛的𝒏次方根的主值。 方根的计算公式 设 𝒛 = 𝒓(𝒄𝒐𝒔𝜽 + 𝒊𝒔𝒊𝒏𝜽),则 𝒘 = 𝒛 𝟏 𝒏 = 𝒓 𝒏 𝒄𝒐𝒔 𝜽 + 𝟐𝒌𝝅 𝒏 + 𝒊𝒔𝒊𝒏 𝜽 + 𝟐𝒌𝝅 𝒏 , 𝒌 ∈ 𝒁

证明:设w=p(cosp+isin)由wn=z,得 p"(cosno isinng)r(cos0 isin0) 则e+2k即p p"=r =VT n0=9+2kmke年2 所以 w-m-Vrc 日+2kr+isin +2kπ ,k∈Z n 。飞由正弦、余弦函数的周期性可知,非零数的 n次方根有n个相异的根
证明: 设𝒘 = 𝝆(𝒄𝒐𝒔𝝋 + 𝒊𝒔𝒊𝒏𝝋) 由𝒘𝒏 = 𝒛 ,得 则 𝝆 𝒏 = 𝒓 𝒏𝝋 = 𝜽 + 𝟐𝒌𝝅 即 𝝆 = 𝒓 𝒏 𝒏𝝋 = 𝜽 + 𝟐𝒌𝝅 , 𝒌 ∈ 𝒁 所以 𝑛次方根有𝑛个相异的根。 由正弦、余弦函数的周期性可知,非零数的 𝝆 𝒏 𝒄𝒐𝒔𝒏𝝋 + 𝒊𝒔𝒊𝒏𝒏𝝋 = 𝒓(𝒄𝒐𝒔𝜽 + 𝒊𝒔𝒊𝒏𝜽) 𝒘 = 𝒛 𝟏 𝒏 = 𝒓 𝒏 𝒄𝒐𝒔 𝜽 + 𝟐𝒌𝝅 𝒏 + 𝒊𝒔𝒊𝒏 𝜽 + 𝟐𝒌𝝅 𝒏 , 𝒌 ∈ 𝒁
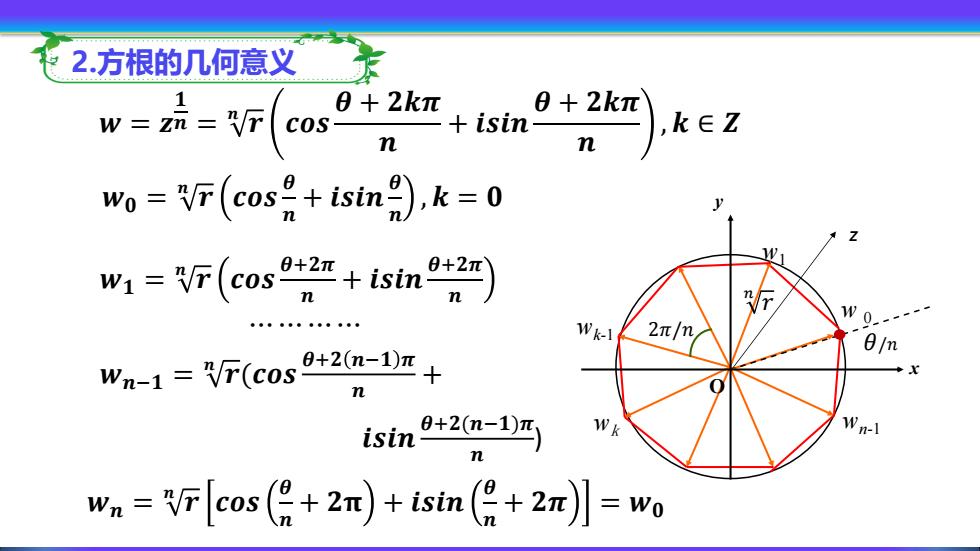
2.方根的几何意义 1 w=z元=VFc0s9 +2kr+isin +2kπ k∈Z n wo =V(cos2+isin g),k=0 W w-(cos +isin 6+2π Wk-1 2π/m 0/m Wn-1=F(cos 0+2(n-1)7 十 +20m-1)严) isin 9 Wn-l wn=F[eos(只+2nm)+ism((+2m=w
2.方根的几何意义 𝜃/𝑛 w1 wk-1 wk wn-1 x y O w 0 z 2𝜋/𝑛 𝒘 = 𝒛 𝟏 𝒏 = 𝒓 𝒏 𝒄𝒐𝒔 𝜽 + 𝟐𝒌𝝅 𝒏 + 𝒊𝒔𝒊𝒏 𝜽 + 𝟐𝒌𝝅 𝒏 , 𝒌 ∈ 𝒁 𝒘𝟎 = 𝒓 𝒏 𝒄𝒐𝒔 𝜽 𝒏 + 𝒊𝒔𝒊𝒏 𝜽 𝒏 , 𝒌 = 𝟎 𝒘𝟏 = 𝒓 𝒏 𝒄𝒐𝒔 𝜽+𝟐𝝅 𝒏 + 𝒊𝒔𝒊𝒏 𝜽+𝟐𝝅 𝒏 𝒘𝒏−𝟏 = 𝒓 𝒏 (𝒄𝒐𝒔 𝜽+𝟐 𝒏−𝟏 𝝅 𝒏 + 𝒊𝒔𝒊𝒏 𝜽+𝟐(𝒏−𝟏)𝝅 𝒏 ) 𝒘𝒏 = 𝒓 𝒏 𝒄𝒐𝒔 𝜽 𝒏 + 𝟐𝛑 + 𝒊𝒔𝒊𝒏 𝜽 𝒏 + 𝟐𝝅 = 𝒘𝟎 ⋯ ⋯ ⋯ ⋯ 𝑟 𝑛