
第三讲 多元函数的偏导数
多元函数微分法及其应用 第三讲 多元函数的偏导数
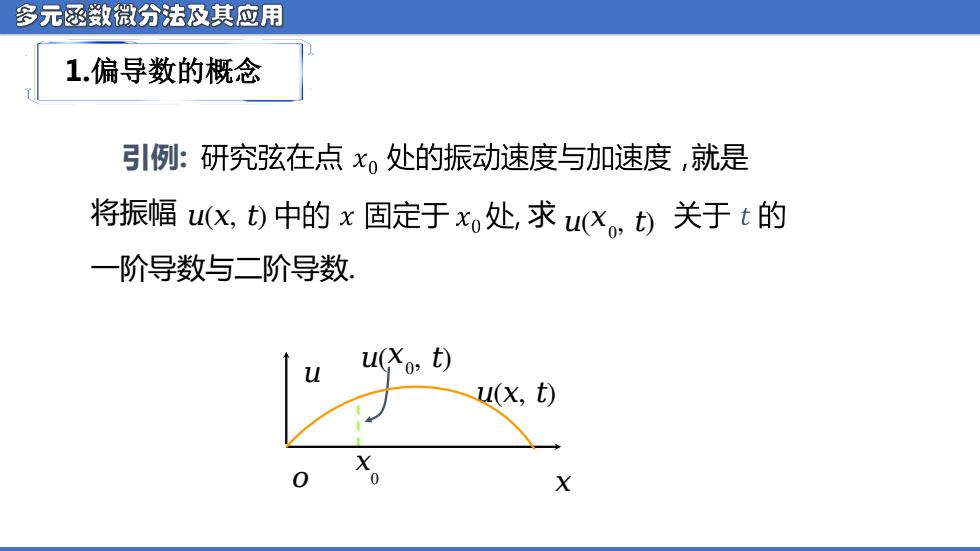
多元函数微分法及其应用 1.偏导数的概念 引例:研究弦在点x处的振动速度与加速度,就是 将振幅u(X,t)中的x固定于x处,求u(心。,t)关于t的 一阶导数与二阶导数 u u(o,t) u(x,t) 0 X
多元函数微分法及其应用 1.偏导数的概念 引例: 就是 ᵆ (ᵆ , ᵆ) ᵆ ᵅ 0 ᵆ ᵆ 求 一阶导数与二阶导数. ᵆ (ᵆ , ᵆ) ᵆ ( ᵆ 0 , ᵆ) ᵆ ( ᵆ 0 将振幅 , ᵆ)

多元函教微分法及其应用 定义1.设函数z=f(x,y)在点(xo,yo) 的某邻域内 极限 lim f(xo +Ax,yo)-f(xo,yo) △X→0 △x 存在,则称此极限为函数之=fxy)在点(Xyo)对x 的偏导数,记为别o,wcw:2小0 f(XVo); 注意: f(XVo) lim f(xo+Ax,yo)-f(xo,yo) df(x,yo) △X→0 △X dx x=x0 f(x。)= lim f(xo+△x)-f(xo) dy △X→0 △X dx =X0
多元函数微分法及其应用 定义1. 存在, ᵆ = ᵅ(ᵆ ,ᵆ ) 在点( ᵆ 0 , ᵆ 0 ) 对ᵆ 的偏导数,记为 的某邻域内 则称此极限为函数 极限 ᵅ ′ ( ᵆ 0 ) = ᵅ ᵆ ( ᵆ 0 , ᵆ 0 ) ; ᵅ ᵆ ( ᵆ 0 , ᵆ 0 ) 注意:

多元函数微分法及其应用 同样可定义对y的偏导数 f (xv)=lim f6+a)-fo,W)=f0,2y=n △y→0 △y dy 若函数z=f(x,y)在域D内每一点(x,y)处对x 或y偏导数存在,则该偏导数称为偏导函数,也简称为 偏导数,记为 0z x’ .2,1w.ig Oz ay' ,名,f.fg af
多元函数微分法及其应用 ᵅ ᵆ ( ᵆ 0 , ᵆ 0 ) 则该偏导数称为偏导函数, 也简称为 偏导数 , ᵅ ᵆ (ᵆ ,ᵆ ) , ᵅ ′ 1(ᵆ ,ᵆ ) ᵅ ᵆ (ᵆ ,ᵆ ) , ᵅ ′ 2(ᵆ ,ᵆ ) 记为

多元函教微分法及其应用 偏导数的概念可以推广到二元以上的函数. 例如,三元函数u=f(x,y,z)在点(x,y,z)处对x的 偏导数定义为 f(x +Ax,y,z)-f(x,y,z) fx(x,y,z)=lim X→0 △X f,(xyz)=? (请自己写出) f,(xyz)=?
多元函数微分法及其应用 偏导数的概念可以推广到二元以上的函数 . ᵅ ᵆ (ᵆ ,ᵆ ,ᵆ ) = ? 偏导数定义为 (请自己写出) ᵅ ᵆ (ᵆ ,ᵆ ,ᵆ ) = ?