
第十二讲 最小二乘法
多元函数微分法及其应用 第十二讲 最小二乘法
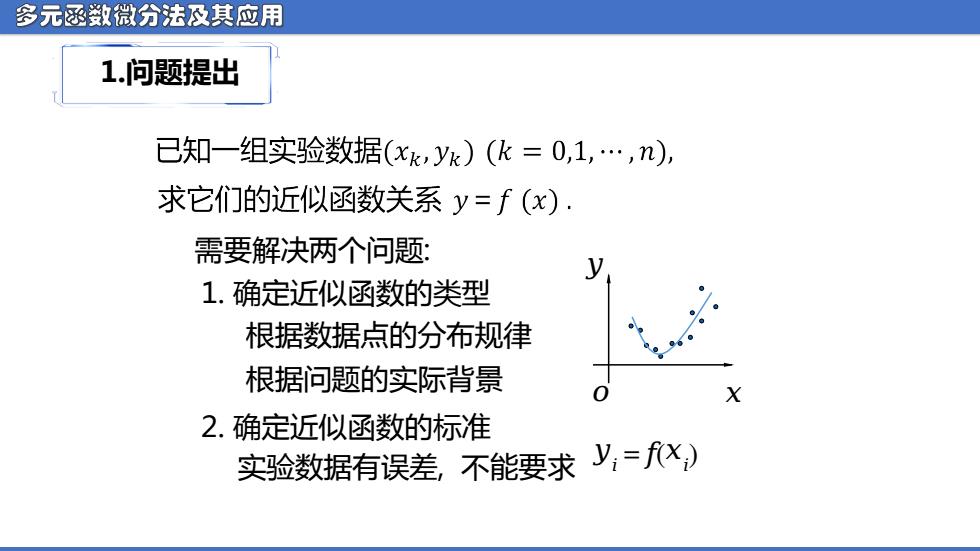
多元函数微分法及其应用 1.问题提出 已知一组实验数据(xk,yk)(k=0,1,.,n), 求它们的近似函数关系y=f(x). 需要解决两个问题: y 1.确定近似函数的类型 根据数据点的分布规律 根据问题的实际背景 X 2.确定近似函数的标准 实验数据有误差,不能要求y,=X,)
多元函数微分法及其应用 1.问题提出 ᵅ ᵆ ᵆ 需要解决两个问题: 1. 确定近似函数的类型 根据数据点的分布规律 根据问题的实际背景 2. 确定近似函数的标准 ᵆ ᵅ = ᵅ( ᵆ ᵅ 实验数据有误差 ) , 不能要求
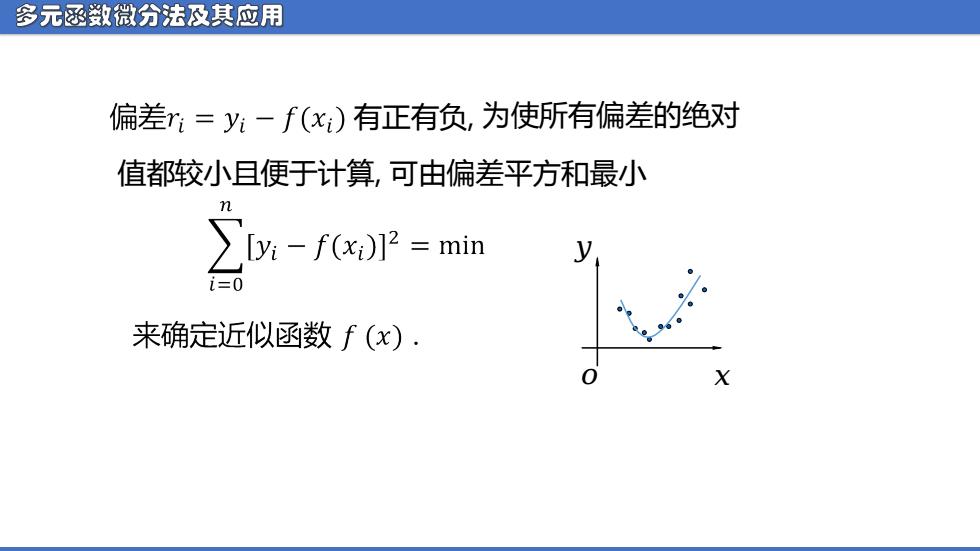
多元函教微分法及其应用 偏差r:=y:-f(x)有正有负,为使所有偏差的绝对 值都较小且便于计算,可由偏差平方和最小 ∑D%-fx)2=min i= 来确定近似函数f(x). X
多元函数微分法及其应用 有正有负, 值都较小且便于计算, 可由偏差平方和最小 为使所有偏差的绝对 ᵅ ᵆ ᵆ
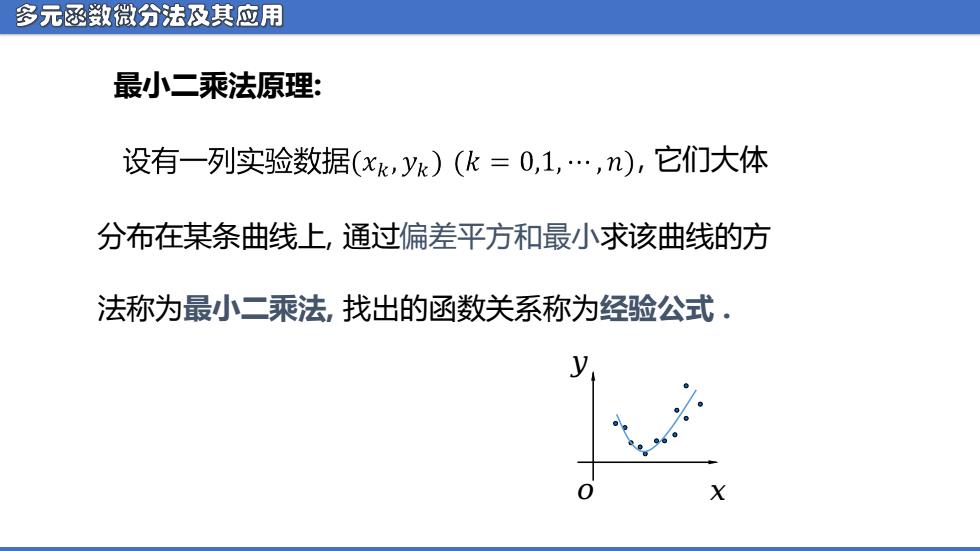
多元函数微分法及其应用 最小二乘法原理: 设有一列实验数据(xk,yk)(k=0,1,.,n),它们大体 分布在某条曲线上,通过偏差平方和最小求该曲线的方 法称为最小二乘法,找出的函数关系称为经验公式. X
多元函数微分法及其应用 最小二乘法原理: 分布在某条曲线上, 通过偏差平方和最小求该曲线的方 法称为最小二乘法, 找出的函数关系称为经验公式 . , 它们大体 ᵅ ᵆ ᵆ

多元函教微分法及其应用 特别,当数据点分布近似一条直线时,问题为确定α,b 使y=ax+b满足: M(ab)= (-axx-b)2 min k三0 da =-2〉(yk-axk-b)xk=0 令 k=0 OM ab =-2(yk-axk-b) =0 称为法方程组 k=0 得 k= 解此线性方程组 xa+m+1)b=∑y 即得a,b k=0
多元函数微分法及其应用 特别, 当数据点分布近似一条直线时, 令 ᵄ (ᵄ ,ᵄ ) = 满足: ᵅ ᵆ ᵆ 得 称为法方程组