
第四讲 正项级数及其收敛法
无 穷 级 数 第四讲 正项级数及其收敛法

无穷级数 1.正项级数的审敛性 0∞ 定义1.若un≥0,则级数 )un称为正项级数! 00 n=1 定理1.正项级数 1 n收敛≤部分和序列Sn(n=1,2,.)有界. n=1 00 证:→若级数 〉un收敛, 则部分和数列{Sn}收敛,故{Sn}有界, n=1 ←一:un≥0,部分和数列{Sn}单调递增,又已知{Sn}有界, 00 故{Sn收敛,从而>un收敛 n=1
无 穷 级 数 1.正项级数的审敛性 则级数 定理1.正项级数 证:
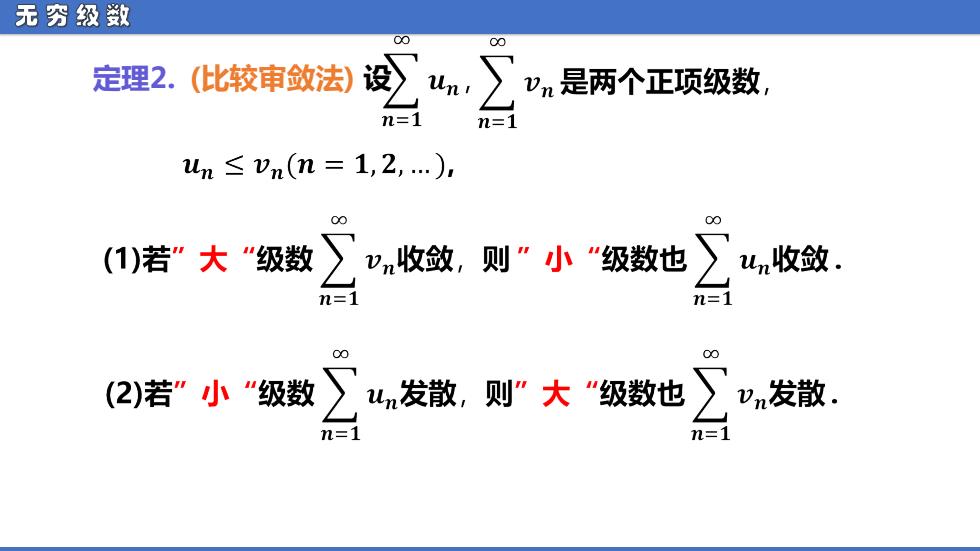
无穷级数 00 定理2.(比较审敛法)设4, vn是两个正项级数, n=1 m.=1 un≤vn(n=1,2,.) 00 (1)若”大“级数〉vn收敛,则"小"级数也) un收敛. n=1 n=1 00 00 (2)若”小“级数∑um发散,则“大“级数也) vn发散。 n=1 n=1
无 穷 级 数 定理2. (比较审敛法) 设

无穷级数 举例 1 例1.判定级数 的敛散性, n=ivn(n+1) 1 1 1 解:“Vnn+万>m+1m+面 n+1 因为级数 1 发散,所以级数 n+1 n=1 1 一也发散
无 穷 级 数 举例 例1. 判定级数 的敛散性. 解: 所以级数

无穷级数 00 推论.(比较审敛法)设 ∑,∑ n是两个正项级数,且存在 n=1 n=1 正整数N,使得当n≥N时,un≤kvn(k>0)成立, (1)若”强“级数)un收敛,则"弱"级数∑也收敛. n=1 n=1 (2)若”弱“级数 un发散,则“强"级数 vn也发散. n=1 n=1
无 穷 级 数 推论. (比较审敛法) 设