
第五讲 主讲人:冀彦 复合函数求导法则
多元函数微分法及其应用 第五讲 复合函数求导法则 主讲人:冀彦
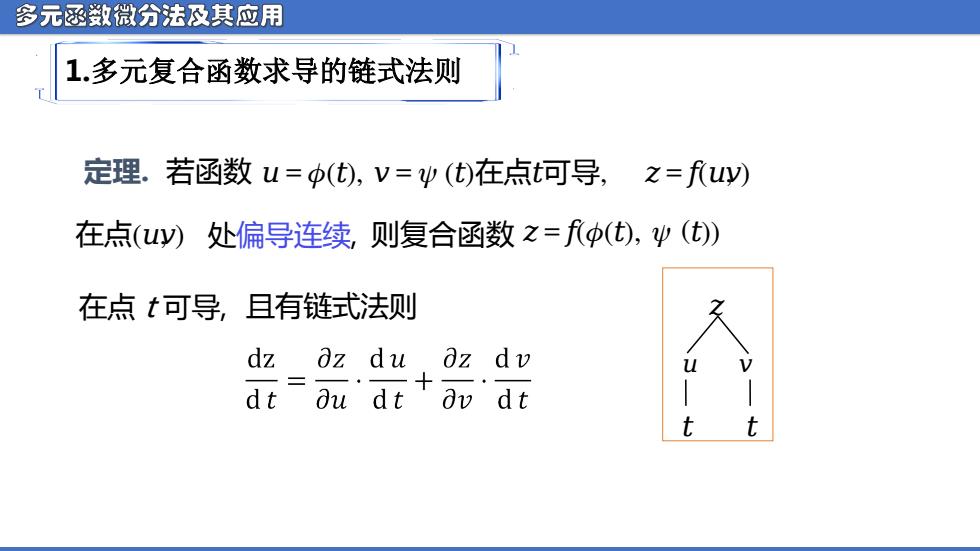
多元函激微分法及其应用 1.多元复合函数求导的链式法则 定理.若函数u=(t),v=妙(t)在点t可导, 之=fuy) 在点(uy)处偏导连续则复合函数之=p(t),ψ(t) 在点t可导,且有链式法则 dz oz du oz dv dt-du dt ov'dt
多元函数微分法及其应用 1.多元复合函数求导的链式法则 ᵆ = ᵅ(ᵱ (ᵆ), ᵱ (ᵆ)) 定理. 若函数 ᵆ = ᵱ (ᵆ), ᵆ = ᵱ (ᵆ)在点ᵆ可导, ᵆ = ᵅ(ᵆ , ) 在点(ᵆ , ) 处偏导连续, 在点 t 可导, ᵆ 则复合函数 且有链式法则 ᵆ ᵆ ᵆ ᵆ

多元函数微分法及其应用 说明: 若定理中f(u,v)在点(u,v)偏导数连续减弱为 偏导数存在,则定理结论不一定成立 u2v 例如:之=fu,v)= u2+2' u2+v2≠0 22 0, u+V=0 u=t,v=t 易知: 9la0)=无0)=0,100y=00)=0 但复合函数之=ft,)= 2 dz1.∂z du oz dv =0.1+0.1=0 du dtav dt
多元函数微分法及其应用 说明: 例如: ᵆ = ᵅ(ᵆ , ᵆ ) = ᵆ = ᵆ , ᵆ = ᵆ 易知: 但复合函数 ᵆ = ᵅ(ᵆ, ᵆ) ≠ =0⋅1+0⋅1= 0 偏导数连续减弱为 偏导数存在, = ᵆ 2 0 , ᵆ 2 + ᵆ 2 = 0 则定理结论不一定成立
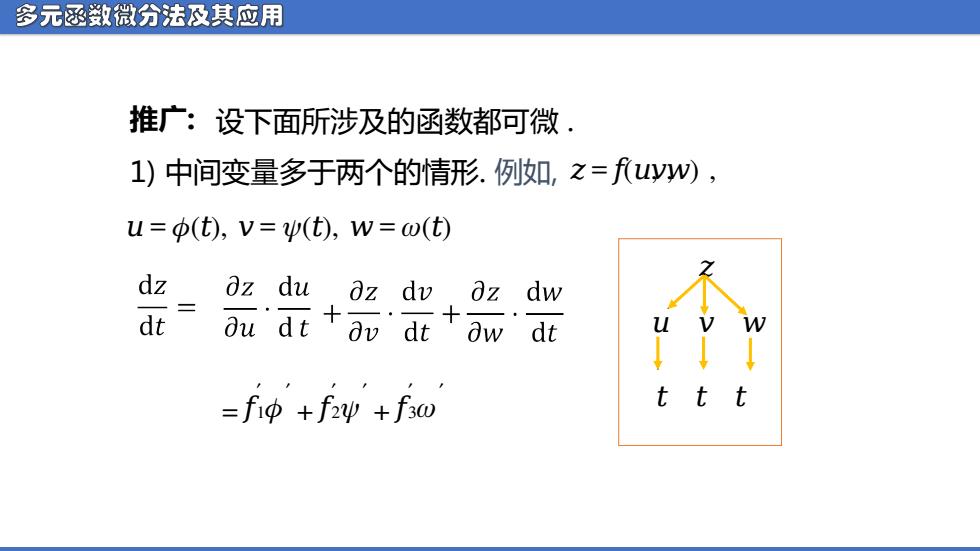
多元函教微分法及其应用 推广:设下面所涉及的函数都可微· 1)中间变量多于两个的情形.例如,之=uyW), u=p(t),V=(t),w=ω(t) t oz du oz dv oz dw du dt +ov'dt ow'dt u ↓↓ =fiφ+fw'+fw ttt
多元函数微分法及其应用 推广: 1) 中间变量多于两个的情形. 例如, ᵆ = ᵅ(ᵆ , ,ᵆ ) , 设下面所涉及的函数都可微 . = ᵅ ′ 1ᵱ ′ + ᵅ ′ 2ᵱ ′ + ᵅ ′ 3ᵱ ′ ᵆ ᵆ ᵆ ᵆ ᵆ ᵆ ᵆ ᵆ = ᵱ (ᵆ), ᵆ = ᵱ (ᵆ), ᵆ = ᵱ (ᵆ)

多元函数微分法及其应用 2)中间变量是多元函数的情形.例如, z=f(uy),u=o(xy),v=v(xy) Oz Oz du oz dv dx =xx=ffa OzOz du oz 0v ay oayaffa
多元函数微分法及其应用 2) 中间变量是多元函数的情形.例如, ᵆ = ᵅ(ᵆ , ) , ᵆ = ᵱ (ᵆ ,ᵆ ), ᵆ = ᵱ (ᵆ ,ᵆ ) = ᵅ ′ 1ᵱ ′ 1 + ᵅ ′ 2ᵱ ′ 1 = ᵅ ′ 1ᵱ ′ 2 + ᵅ ′ 2ᵱ ′ 2 ᵆ ᵆ ᵆ ᵆ ᵆ ᵆ ᵆ