
第六讲 空间直线
向量代数与空间解析几何 第六讲 空间直线
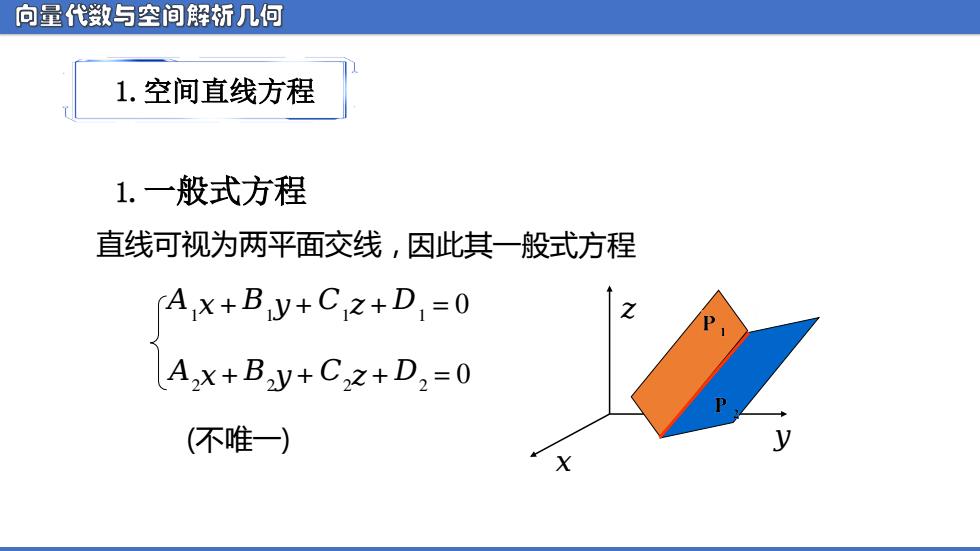
向量代数与空间解析几何 1.空间直线方程 1.一般式方程 直线可视为两平面交线,因此其一般式方程 Ax+By+Cz+D=0 Azx+By+Cxz+D2=0 (不唯一)) X
向量代数与空间解析几何 1.空间直线方程 1. 一般式方程 直线可视为两平面交线,因此其一般式方程 ᵃ 1 ᵆ + ᵃ 1 ᵆ + ᵃ 1 ᵆ + ᵃ 1 = 0 ᵃ 2 ᵆ + ᵃ 2 ᵆ + ᵃ 2 ᵆ + ᵃ 2 = 0 (不唯一) ᵆ ᵆ ᵆ

向量代数与空间解析几何 2.对称式方程 已知直线上一点Mo(xo,yo,Zo)和它的方向向量 3=(m,n,p),设直线上的动点为M(x,y,z) 则MoM/3 M(xyz) 故有 x-xo y-yo Z-Z0 m m /MXy3) 此式称为直线的对称式方程(也称为点向式方程) 说明:某些分母为零时,其分子也理解为零 例如,当m=n=0,卫≠0时,直线方程为
向量代数与空间解析几何 ᵄ 0 ( ᵆ 0 , ᵆ 0 , ᵆ 0 ) 2. 对称式方程 故有 说明: 某些分母为零时, 其分子也理解为零. 则 ᵄ (ᵆ ,ᵆ ,ᵆ) 此式称为直线的对称式方程(也称为点向式方程) 直线方程为 和它的方向向量

向量代数与空间解析几何 3.参数式方程 设 x-0y-0=Z-Z0=t m m p 得参数式方程: X=X。+t y=yo+rt 之=20+屯
向量代数与空间解析几何 3. 参数式方程 设 得参数式方程 : ᵆ = ᵆ 0 + ᵅᵆ ᵆ = ᵆ 0 + ᵅᵆ ᵆ = ᵆ 0 + ᵅᵆ

向量代数与空间解析几何 例1.用对称式及参数式表示直线 x+y+z+1=0 2x-y+3z+4=0 解先在直线上找一点, 令x=1,解方程组 Jy+2=-2 1y-3z=6 得y=0,2=-2,故(1,0,-2)是直线上一点 再求直线的方向向量,已知直线的两平面的法向量为 n=(1,1,1),n2=(2,-1,3)31n,31n2
向量代数与空间解析几何 例1.用对称式及参数式表示直线 解:先在直线上找一点. ᵆ + ᵆ = − 2 ᵆ − 3ᵆ = 6 得 ᵆ = 0, ᵆ = − 2, 已知直线的两平面的法向量为