
第二讲 空间直角坐标系
向量代数与空间解析几何 第二讲 空间直角坐标系

向量代数与空问解析几何 1.空间直角坐标系 1.空间直角坐标系的基本概念 过空间一定点0,由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系。 z轴(竖轴) ·坐标原点 ·坐标轴 IV 0z面 ·坐标面 ·卦限(八个) 0X02面 vI y轴(纵轴) x轴(横轴) VI VIIⅢ
向量代数与空间解析几何 Ⅶ Ⅲ Ⅱ Ⅵ Ⅷ Ⅴ Ⅳ 1.空间直角坐标系 由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系. • 坐标原点 • 坐标轴 • 坐标面 • 卦限(八个) zox面 1. 空间直角坐标系的基本概念 Ⅰ
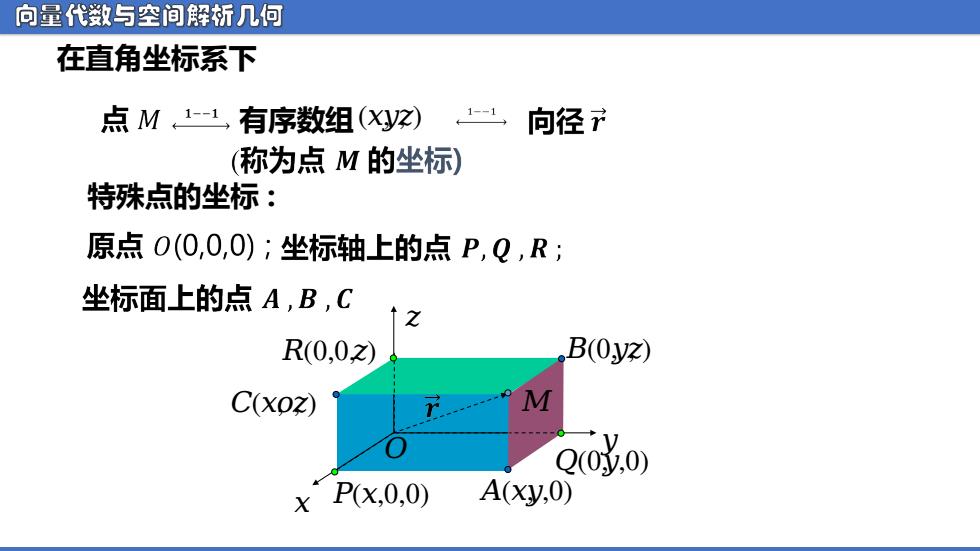
向量代数与空间解析几何 在直角坐标系下 点M,1-1有序数组(Xy)1 向径 (称为点M的坐标) 特殊点的坐标: 原点O(0,0,0);坐标轴上的点P,Q,R; 坐标面上的点A,B,C R(0,0,2) B(0y) C(xoz) M o成.0) xPx,0,0) A(xy,0)
向量代数与空间解析几何 ᵄ ᵆ ᵆ ᵆ 在直角坐标系下 特殊点的坐标 : 有序数组(ᵆ ,ᵆ ,ᵆ ) ᵄ (ᵆ ,0,0) ᵄ (0,ᵆ ,0) ᵄ (0,0,ᵆ ) ᵃ (ᵆ ,ᵆ ,0) ᵃ (0,ᵆ ,ᵆ ) ᵃ (ᵆ ᵅ, ,ᵆ ) ᵄ

向量代数与空间解析几何 坐标轴: y=0 X轴 2=0 y轴 之=0 X=0 坐标面: ≥轴4 X=0 0y面之=0 y=0 面X=0 0x面→y=0
向量代数与空间解析几何 坐标轴 : ᵆ 轴↔ ᵆ = 0 ᵆ = 0 ᵆ = 0 ᵆ = 0 ᵆ 轴↔ ᵆ 轴↔ ᵆ = 0 ᵆ = 0 坐标面 : ᵆᵅᵆ 面↔ᵆ = 0 ᵆᵅᵆ 面 ↔ᵆ = 0 ᵆᵅᵆ 面 ↔ᵆ = 0 ᵆ ᵆ ᵆ

向量代数与空间解析几何 2.向量的坐标表示 在空间直角坐标系下,任意向量可用向径OM表示. 以,j,k,分别表示x,y,z轴上的单位向量,设点M 的坐标为M(Xyz),则 OM-ON+NM =0A+0B+OC M B =x元+yi+zk=(Xyz) 此式称为向量产的坐标分解式 N X xi,yj,zk称为向量?沿三个坐标轴方向的分向量
向量代数与空间解析几何 2. 向量的坐标表示 在空间直角坐标系下, ᵄ (ᵆ ,ᵆ ,ᵆ ), 则 沿三个坐标轴方向的分向量. = (ᵆ ,ᵆ ,ᵆ ) ᵆ ᵅ ᵆ ᵆ ᵄ ᵄ ᵃ ᵃ ᵃ 的坐标为 此式称为向量 r 的坐标分解式