
第一讲 向量及其线性运算
向量代数与空间解析几何 第一讲 向量及其线性运算
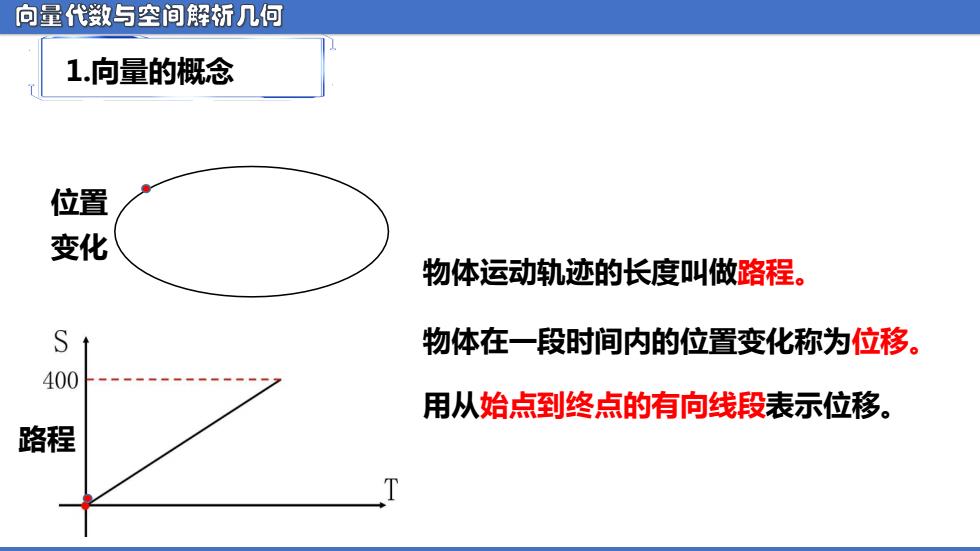
向量代数与空间解析几何 1.向量的概念 位置 变化 物体运动轨迹的长度叫做路程。 S 物体在一段时间内的位置变化称为位移。 400 用从始点到终点的有向线段表示位移。 路程 T
向量代数与空间解析几何 物体运动轨迹的长度叫做路程。 物体在一段时间内的位置变化称为位移。 用从始点到终点的有向线段表示位移。 1.向量的概念 路程 位置 变化

向量代数与空间解析几何 一.向量的概念 向量:既有大小,又有方向的量称为向量(又称矢量). 表示法:有向线段AB,或a, 向量的模:向量的大小,记作AB,或a 向量的方向 d B 向径(矢径):起点为原点的向量。 自由向量:与起点无关的向量。 向量的大小 单位向量:模为1的向量,记作°或a°. 零向量:模为0的向量
向量代数与空间解析几何 一.向量的概念 表示法: 向量的模 : 向量的大小, 向量: 既有大小, 又有方向的量称为向量 (又称矢量). 向径 (矢径): 自由向量: 与起点无关的向量. 起点为原点的向量. 单位向量: 零向量: 模为 0 的向量. A 向量的方向 B 向量的大小
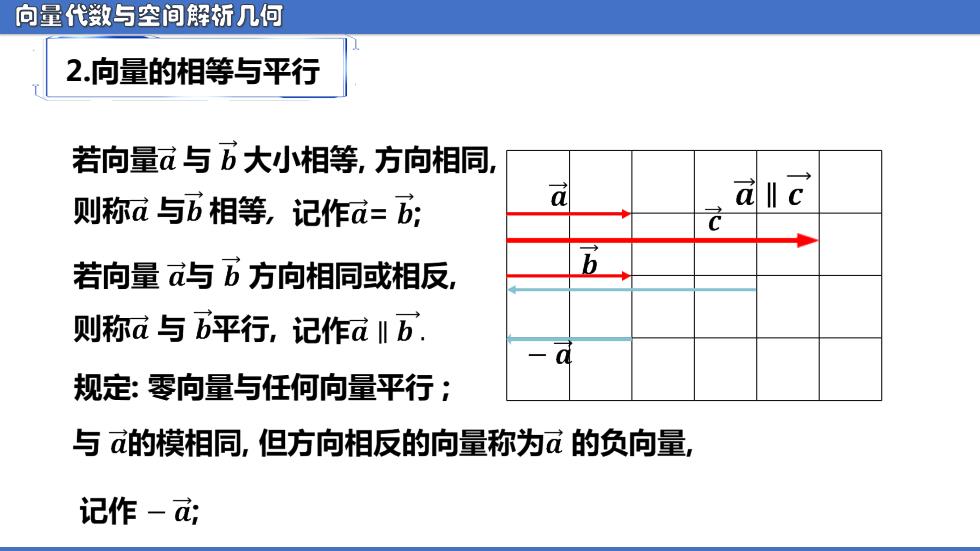
向量代数与空间解析几何 2.向量的相等与平行 若向量a与b大小相等,方向相同, 则称a与b相等,记作d=; a al 若向量与b方向相同或相反, 五 则称a与b平行,记作aⅡb. 规定:零向量与任何向量平行; 与的模相同,但方向相反的向量称为a的负向量, 记作-;
向量代数与空间解析几何 规定: 零向量与任何向量平行 ; 2.向量的相等与平行
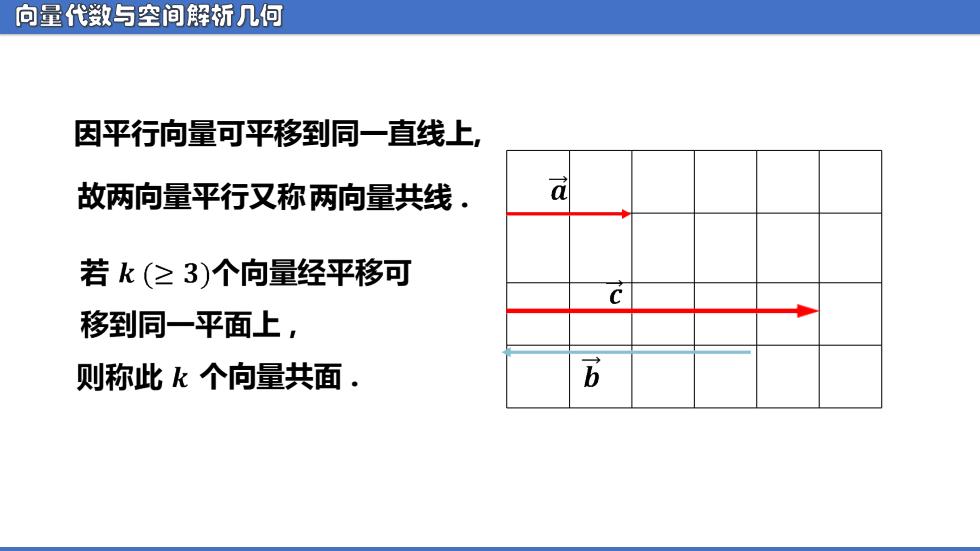
向量代数与空间解析几何 因平行向量可平移到同一直线上, 故两向量平行又称两向量共线· d 若k(≥3)个向量经平移可 c 移到同一平面上 则称此k个向量共面. 6
向量代数与空间解析几何 因平行向量可平移到同一直线上, 故两向量平行又称两向量共线 . 个向量共面