
第四讲 定积分的在物理上的应用
第四讲 定积分的在物理上的应用

定积分及其应用 一、定积分在物理上的应用 1、 复习旋转体体积 2、 变力做功问题 3、 水压力 4、 引力
复习旋转体体积 一、定积分在物理上的应用 1、 3、 水压力 2、 变力做功问题 4、 引力
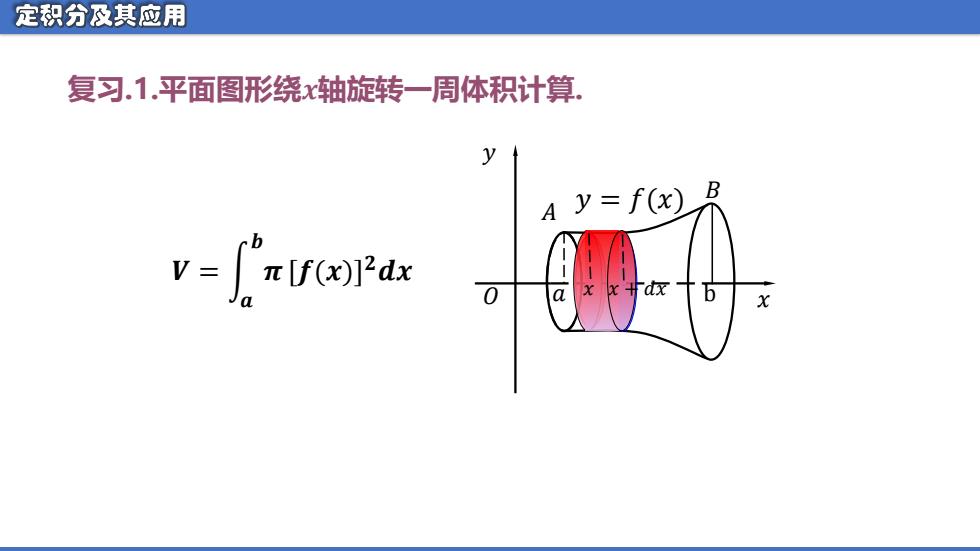
定积分及其应用 复习.1.平面图形绕x轴旋转一周体积计算。 y A y=f(x)B v=miePux b a b
复习.1.平面图形绕𝒙轴旋转一周体积计算. 𝑽 = න 𝒂 𝒃 𝝅[𝒇(𝒙)] 𝟐𝒅𝒙 𝑎 𝑥 b 𝑥 𝑦 𝑥 + 𝑑𝑥 𝐵 𝐴 𝑂 𝑦 = 𝑓(𝑥)

定积分及其应用 复习.2.平面图形绕y轴旋转一周体积计算 由曲线x=p(y)、直线y=c,y=d(c<d)与y轴所围成的 曲边梯形绕y轴旋转一周而成的旋转体的体积为 v=πp'dy +dy x=o(y)
复习.2.平面图形绕𝒚轴旋转一周体积计算. 由曲线 𝒙 = 𝝋(𝒚) 、 直线 𝒚 = 𝑐, 𝑦 = 𝑑(𝑐 < 𝑑)与𝒚 轴所围成的 曲边梯形,绕𝒚轴旋转一周而成的旋转体的体积为 𝑉 = 𝜋 න 𝑐 𝑑 [𝜑(𝑦)] 2 𝑑𝑦 𝑦 𝑂 𝑥 𝑐 𝑑 𝑥 = 𝜑(𝑦) 𝑦 𝑦 + 𝑑𝑦
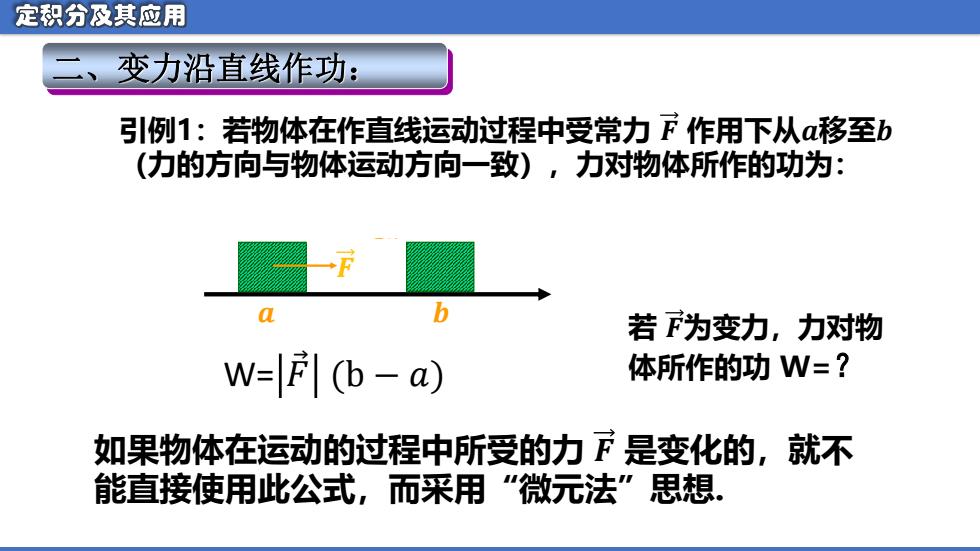
定积分及其应用 变力沿直线作功: 引例1:若物体在作直线运动过程中受常力下作用下从移至b (力的方向与物体运动方向一致),力对物体所作的功为: 若下为变力,力对物 W=F (b-a) 体所作的功W=? 如果物体在运动的过程中所受的力下是变化的,就不 能直接使用此公式,而采用“微元法”思想
二、变力沿直线作功: 引例1:若物体在作直线运动过程中受常力 𝑭 作用下从𝒂移至𝒃 (力的方向与物体运动方向一致),力对物体所作的功为: 𝒂 𝒃 F 若 𝑭为变力,力对物 体所作的功 W=? 如果物体在运动的过程中所受的力 𝑭 是变化的,就不 能直接使用此公式,而采用“微元法”思想. W= 𝐹 Ԧ (b − 𝑎) 𝑭