
第二讲 旋转体的体积
第二讲 旋转体的体积

定积分及其应用 一、定积分的应用 1、复习平面图形面积的求法 2、定积分在几何上的应用 3、定积分在物理上的应用
1、 复习平面图形面积的求法 3、 定积分在物理上的应用 2、 定积分在几何上的应用 一、定积分的应用
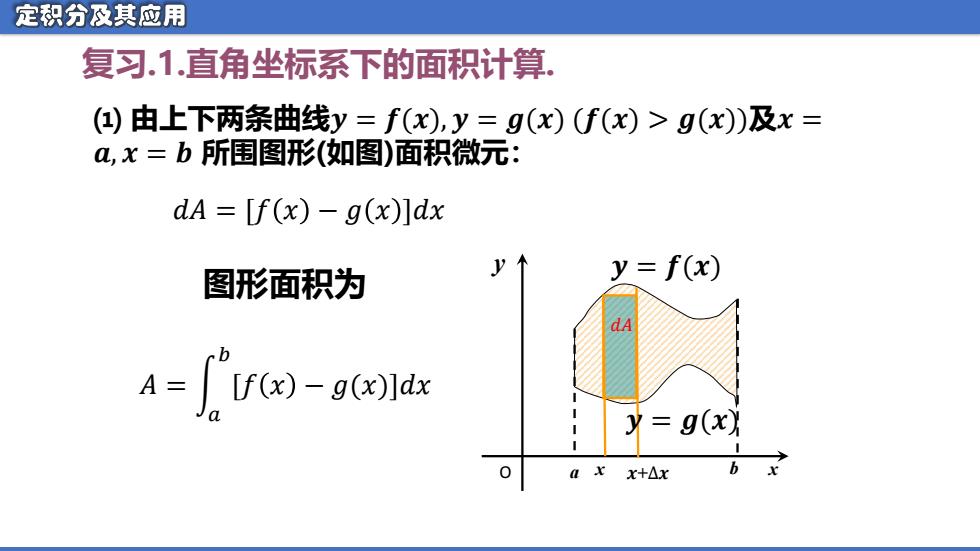
定积分及其应用 复习.1.直角坐标系下的面积计算. (1)由上下两条曲线y=f(x),y=g(x)f(x)>g(x)及x= α,x=b所围图形(如图)面积微元: dA=[f(x)-g(x)]dx 图形面积为 y=f(x) dA A=If(x)-g(x)ldx =g@i arx+△x
复习.1.直角坐标系下的面积计算. ⑴ 由上下两条曲线𝒚 = 𝒇(𝒙), 𝒚 = 𝒈(𝒙) (𝒇(𝒙) > 𝒈(𝒙))及𝒙 = 𝒂, 𝒙 = 𝒃 所围图形(如图)面积微元: 图形面积为 O 𝒚 = 𝒈(𝒙) y 𝒚 = 𝒇(𝒙) a x 𝒙+∆𝒙 b x 𝑑𝐴 = [𝑓 𝑥 − 𝑔 𝑥 ]𝑑𝑥 𝐴 = න 𝑎 𝑏 [𝑓 𝑥 − 𝑔(𝑥)]𝑑𝑥 𝑑𝐴

定积分及其应用 2.直角坐标系下的面积计算, 由左右两条曲线x=p(y),x=(y)及x=c,x=d所围图 形(如图)面积微元 dA =((y)-v(y))dy y d 图形面积为 =(y) x=o(y) A=[00y-6]a y+dy dA X
2.直角坐标系下的面积计算. 由左右两条曲线𝒙 = 𝝋 𝒚 , 𝒙 = 𝝍(𝒚)及𝒙 = 𝒄, 𝒙 = 𝒅所围图 形(如图)面积微元 图形面积为 O 𝑥 𝑦 𝑑 𝑦 + 𝑑𝑦 𝑦 𝑐 𝒙 = 𝝍(𝒚) 𝒙 = 𝝋 𝒚 𝑑𝐴 = (𝝋 𝒚 − 𝝍(𝒚))𝑑𝑦 𝐴 = න 𝑐 𝑑 [ 𝝋 𝒚 − 𝝍(𝒚)]𝑑𝑦 𝑑𝐴
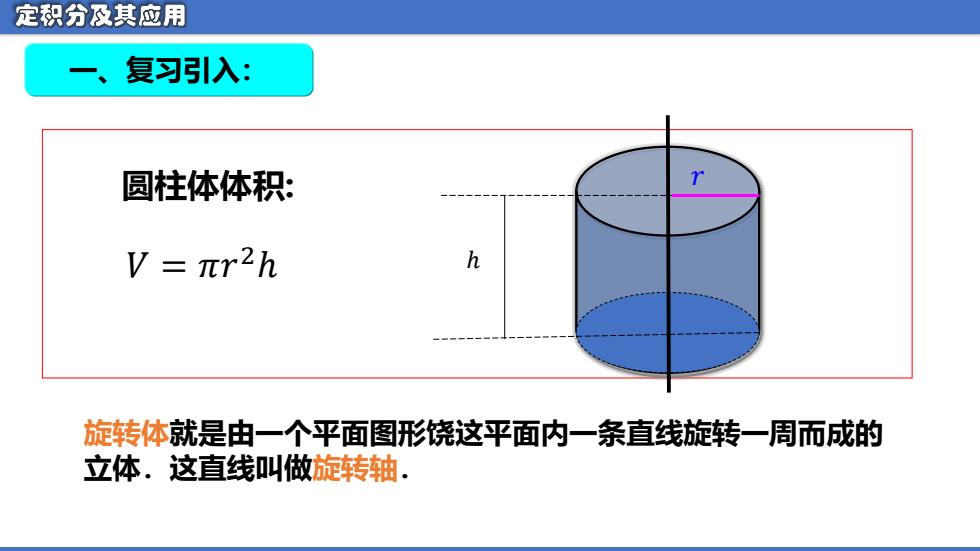
定积分及其应用 复习引入: 圆柱体体积: V=πr2h h 旋转体就是由一个平面图形饶这平面内一条直线旋转一周而成的 立体.这直线叫做旋转轴
一、复习引入: 圆柱体体积: ℎ 𝑟 旋转体就是由一个平面图形饶这平面内一条直线旋转一周而成的 立体.这直线叫做旋转轴. 𝑉 = 𝜋𝑟 2ℎ