
第九讲 空间曲线
向量代数与空间解析几何 第九讲 空间曲线
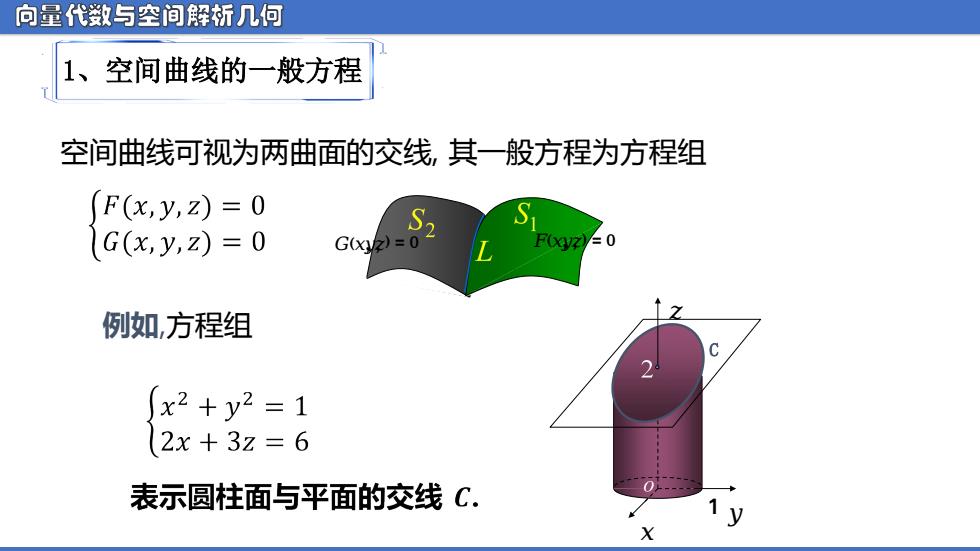
向量代数与空间解析几何 1、空间曲线的一般方程 空间曲线可视为两曲面的交线,其一般方程为方程组 F(x,y,Z)=0 G(x,y,z)=0 S2 G(XZ)= F(Z)=0 例如,方程组 x2+y2=1 2x+3z=6 表示圆柱面与平面的交线C
向量代数与空间解析几何 1、空间曲线的一般方程 空间曲线可视为两曲面的交线, 其一般方程为方程组 例如,方程组 ᵃ (ᵆ ,ᵆ ,ᵆ ) = 0 ᵃ (ᵆ ,ᵆ ,ᵆ ) = 0 ᵆ ᵆ ᵆ 1 C
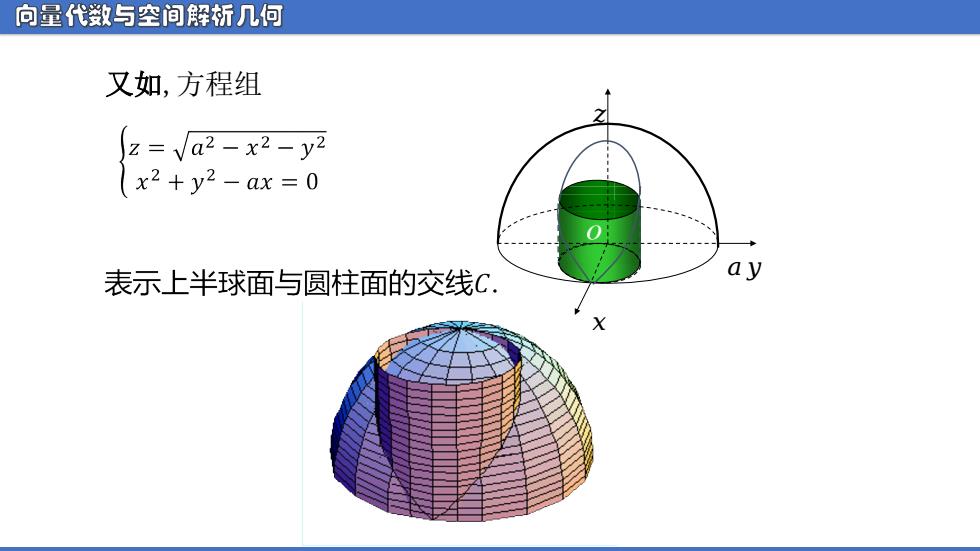
向量代数与空间解析几何 又如,方程组 z=a2-x2-y2 x2+y2-ax=0 表示上半球面与圆柱面的交线C. ay
向量代数与空间解析几何 又如,方程组 ᵆ ᵆ ᵆ ᵄ

向量代数与空间解析几何 2.空间曲线的参数方程 将曲线C上的动点坐标x,y,z表示成参数t的函数: x=x(t) y=y(t) 称它为空间曲线的参数方程 z=2(t) 例如,圆柱螺旋线的参数方程为 M X y
向量代数与空间解析几何 2.空间曲线的参数方程 称它为空间曲线的参数方程. ᵆ = ᵆ (ᵆ) ᵆ = ᵆ (ᵆ) ᵆ = ᵆ (ᵆ) 例如,圆柱螺旋线的参数方程为 ᵆ ᵆ ᵆ ᵰ ᵄ
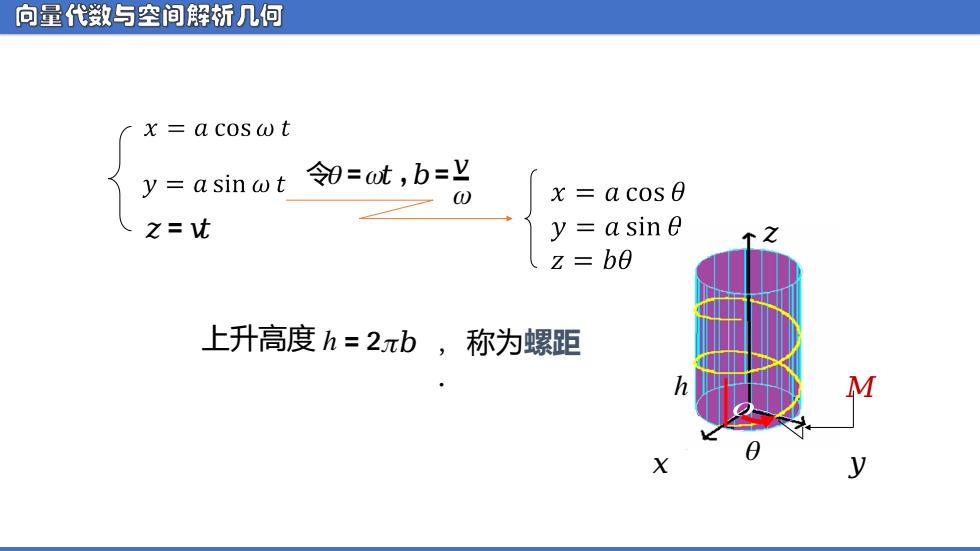
向量代数与空间解析几何 x =acoswt y=asinwt 令0=wt,b=y 0) x=acos0 之=t a sin0 个之 z=b0 上升高度h=2πb,称为螺距 M X y
向量代数与空间解析几何 令ᵰ =ᵱ ᵆ ,ᵄ = ᵆ ᵱ ℎ = 2ᵰ ᵄ ᵆ = ᵆᵆ 上升高度 , 称为螺距 . ᵆ ᵆ ᵆ ᵰ ℎ ᵄ