
第六讲 无穷限的反常积分
第六讲 无穷限的反常积分
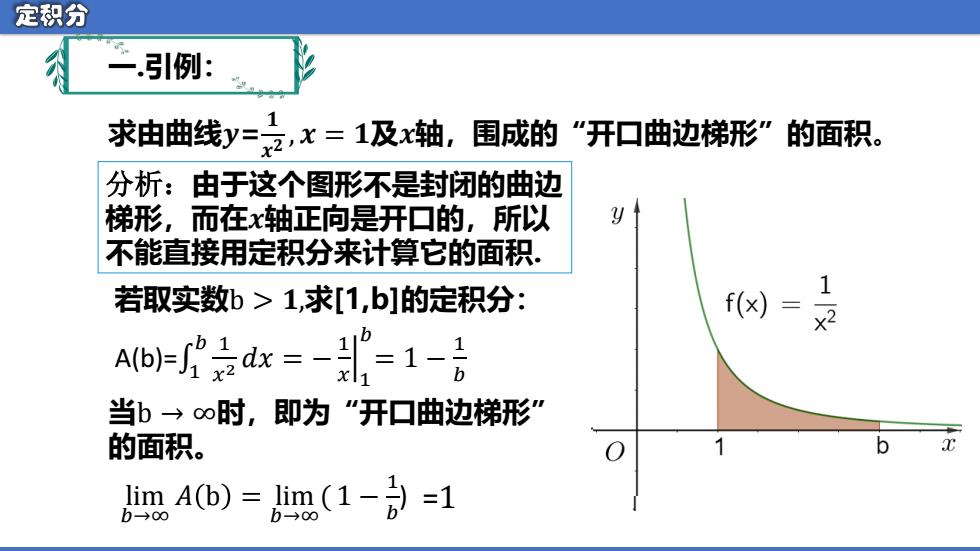
定积分 一引例: 求由曲线y=2,x=1及x轴, 围成的“开口曲边梯形”的面积。 分析:由于这个图形不是封闭的曲边 梯形,而在x轴正向是开口的,所以 不能直接用定积分来计算它的面积. 若取实数b>1,求[1,b]的定积分: f(x)= 1 AMb=是dx=-=1-吉 当b→∞时,即为“开口曲边梯形 的面积。 b m4(b)=m(1-方=1
求由曲线𝒚= 𝟏 𝒙 𝟐 , 𝒙 = 𝟏及𝒙轴,围成的“开口曲边梯形”的面积。 A(b)=1 𝑏 1 𝑥 2 𝑑𝑥 = − ቚ 1 𝑥 1 𝑏 = 1 − 1 𝑏 lim 𝑏→∞ 𝐴 b = lim 𝑏→∞ ( 1 − 1 𝑏 ) =1 分析:由于这个图形不是封闭的曲边 梯形,而在𝒙轴正向是开口的,所以 不能直接用定积分来计算它的面积. 若取实数b > 𝟏,求[1,b]的定积分: 当b → ∞时,即为“开口曲边梯形” 的面积。 一.引例:

定积分 这个极限称为函数y=立,在无穷区间1,+∞) 上的积分,记为是dx.由于它已不是普通意义 上的定积分,因此我们把它称为广义积分. 也就是说函数在y=之无穷区间[1,+o)上的广义积分, 就是函数y=克在区间1,b1上的定积分当b→+∞ 时的极限“是dx
这个极限称为函数y = 𝟏 𝒙 𝟐 , 在无穷区间[𝟏, +∞) 上的积分,记为�� +∞ 𝟏 𝒙 𝟐 𝒅𝒙. 由于它已不是普通意义 无穷区间[𝟏, +∞) 就是函数y = 𝟏 𝒙 𝟐 在区间[𝟏, 𝒃]上的定积分当𝒃 → +∞ ��时的极限 +∞ 𝟏 𝒙 𝟐 𝒅𝒙. 上的定积分,因此我们把它称为广义积分. 也就是说函数在y = 𝟏 𝒙 𝟐 上的广义积分

定积分 、无穷限的反常积分: 定义1:设函数f(x)在区间[a,+∞)上连续,取b>a,如果极限: 1im∫f(x)dx存在,则称此极限为函数f(x)在无穷区间 +00 [a,+o)上的反常积分,记作:t”f(x)dx 十00 、f(x)d=lim fx)dr b→+∞Ja 当极限存在时,称反常积分收敛; 当极限不存在时,称反常积分发散
二、无穷限的反常积分: 定义1:设函数𝒇(𝒙)在区间[𝒂, +∞)上连续,取𝒃>a,如果极限: lim 𝑏→+∞ �� 𝑏 f 𝑥 𝑑𝑥 存在,则称此极限为函数𝒇(𝒙)在无穷区间 a +∞ 𝑓 𝑥 𝑑𝑥 න a +∞ 𝑓 𝑥 𝑑𝑥 = lim 𝑏→+∞ න 𝑎 𝑏 f 𝑥 𝑑𝑥 当极限存在时,称反常积分收敛; [𝒂, +∞)上的反常积分,记作: 当极限不存在时,称反常积分发散

定积分 定义2:设函数f(x)在区间(-∞,b]上连续,取a<b,如果极限: 1im也f(x)dx存在,则称此极限为函数f)在无穷区间 (-o,b]上的反常积分,记作:」也f(x)dx [°f6x)dx=mfcd 当极限存在时,称反常积分收敛: 当极限不存在时,称反常积分发散
定义2:设函数𝒇(𝒙)在区间(−∞,𝒃]上连续,取𝒂 <b,如果极限: lim 𝑎→−∞ �� 𝑏 f 𝑥 𝑑𝑥 存在,则称此极限为函数𝒇(𝒙)在无穷区间 ∞− 𝑏 𝑓 𝑥 𝑑𝑥 න −∞ 𝑏 𝑓 𝑥 𝑑𝑥 = lim 𝑎→−∞ න 𝑎 𝑏 f 𝑥 𝑑𝑥 当极限存在时,称反常积分收敛; (−∞, 𝒃]上的反常积分,记作: 当极限不存在时,称反常积分发散