
第一讲 常数项级数的概念
无 穷 级 数 第一讲 常数项级数的概念

无穷级数 1.常数项级数的概念 引例1.用圆内接正多边形面积逼近圆面积 依次作圆内接正3×2”(n=0,1,2,.)边形,设ao表示内接正三角 形面积,αk表示边数增加时增加的面积, 则圆内接正3×2n边形面积为 a+a1+a2+.+an 当n→oo时,这个和逼进于圆的面积 即 A=a0+a1+.+an+
无 穷 级 数 1.常数项级数的概念 引例1. 用圆内接正多边形面积逼近圆面积 ᵈ ᵼ + ⋯ 即
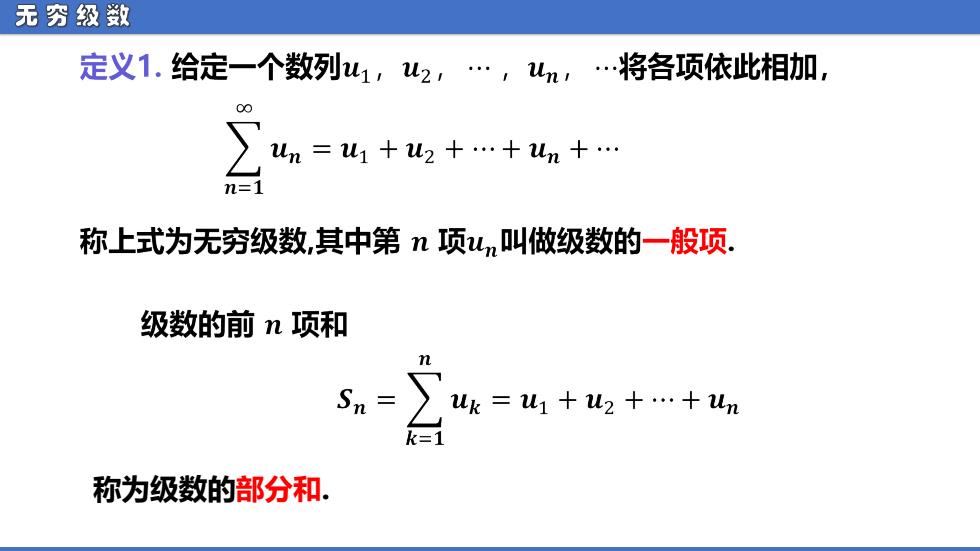
无穷级数 定义1.给定一个数列u1,u2,.,.将各项依此相加, 00 un=u1+u2+.+un+ n=1 称上式为无穷级数,其中第n项um叫做级数的一般项. 级数的前n项和 Sn= uk=u1+u2+.+un k=1 称为级数的部分和
无 穷 级 数 称为级数的部分和

无穷级数 2.无穷级数的收敛与发散 若lim Sn=S存在,则称无穷级数收敛,并称S为级数的和,记作 11→00 ●0 n=1 称差值rn=S-Sn=un+1十un+2+.为级数的余项. limrn 0 九→oo 若lim Sn不存在, 则称无穷级数发散. 1→0o
无 穷 级 数 则称无穷级数发散. 2.无穷级数的收敛与发散

无穷级数 举例 例1.判定下列级数的敛散性 份”) lim 0 1 ·lim Sn=1,所以该级数收敛。 1<1 n→o∞ 9=
无 穷 级 数 举例 例1. 判定下列级数的敛散性. 解: (1) ᵉ = ᵼ ᵽ < ᵼ