
第十章 重积分
重积分 第十章 重 积 分

第六讲 三重积分的计算
重积分 第六讲 三重积分的计算
重积分 1柱坐标计算三重积分 设M(x,y,z)∈R3,将x,y用极坐标p,代替,则(p,0,z) 就称为点M的柱坐标.直角坐标与柱面坐标的关系: x=pcos0 0≤p<+∞ y=psin0 0≤0≤2π -0∞<Z<十∞ z=Z M(,y,z) 坐标面分别为 p=常数 圆柱面 +V 0=常数 半平面 (x,y,0) z=常数 平面
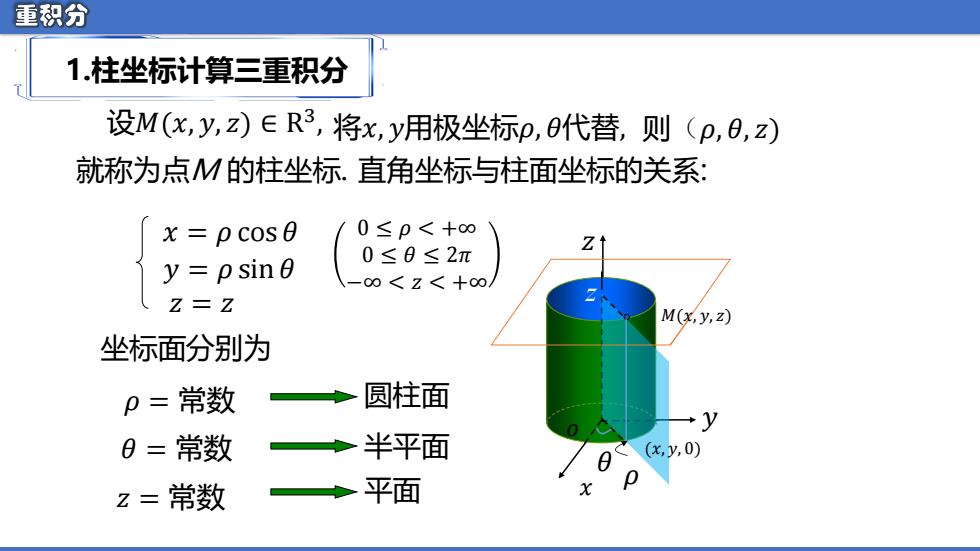
重积分 1.柱坐标计算三重积分 o 𝑥 𝑦 𝑧 设𝑀(𝑥, 𝑦, 𝑧) ∈ R 3 , 将𝑥, 𝑦用极坐标𝜌, 𝜃代替, 则(𝜌, 𝜃, 𝑧) 就称为点M 的柱坐标. 0 ≤ 𝜌 < +∞ 0 ≤ 𝜃 ≤ 2𝜋 −∞ < 𝑧 < +∞ 𝑦 = 𝜌 sin 𝜃 𝑧 = 𝑧 𝑥 = 𝜌 cos 𝜃 直角坐标与柱面坐标的关系: 𝜌 = 常数 坐标面分别为 圆柱面 𝜃 = 常数 半平面 𝑧 = 常数 平面 𝑜 𝜃 z 𝑀(𝑥, 𝑦, 𝑧) 𝜌 (𝑥, 𝑦, 0)

重积分 如图所示,在柱面坐标系中体积元素为 dv=pdpdedz pd0 因此 ∬nfx,y,2)du =jnF(p,日,z)pdpd8dz 其中F(p,0,Z)=f(pcos0,psin8,z) 适用范围: 1)积分域表面用柱面坐标表示时方程简单; 2)被积函数用柱面坐标表示时变量互相分离
重积分 如图所示, 在柱面坐标系中体积元素为 z 𝜌 d 𝑧 d 𝜌 𝜌 d 𝜃 𝜃 d 𝑣 = 𝜌 d 𝜌 d 𝜃 d 𝑧 因此 ʃʃʃΩ 𝑓(𝑥, 𝑦, 𝑧) d 𝑣 = ʃʃʃΩ𝐹(𝜌, 𝜃, 𝑧)𝜌 d 𝜌 d 𝜃 d 𝑧 其中 𝐹(𝜌, 𝜃, 𝑧) = 𝑓(𝜌 cos 𝜃 , 𝜌 sin 𝜃 , 𝑧) 适用范围: 1) 积分域表面用柱面坐标表示时方程简单 ; 2) 被积函数用柱面坐标表示时变量互相分离. 𝑥 𝑦 𝑧 o d 𝜌 𝑑𝜃

重积分 例1.计算三重积分z√x2+y2 dxdydz其中2为由 柱面x2+y2=2x及平面z=0,z=a(a>0),y=0所围 成半圆柱体 0≤p≤2cos 解:在柱面坐标系下2: Z 0≤0≤2 原式=nzp2dpd0dz 0≤z≤a 0人 |2 2c0s0 2 p=2 cos0 zdz de p2dp 4a2 π/ 2 cos3 0de 8 9=ga3 dv=pdpdθdz
重积分 例1. 计算三重积分 其中为由 𝑥 2 + 𝑦 2 = 2𝑥 𝑧 = 0, 𝑧 = 𝑎 (𝑎 > 0), 𝑦 = 0 所围 解: 在柱面坐标系下 න 0 2 cos 𝜃 𝜌 2 d 𝜌 = 4𝑎 2 3 න 0 ൗ 𝜋 2 cos3 𝜃 d 𝜃 Ω: 0 ≤ 𝜌 ≤ 2 cos 𝜃 0 ≤ 𝜃 ≤ 𝜋 2 0 ≤ 𝑧 ≤ 𝑎 及平面 2 𝑎 𝑥 𝑦 𝑧 𝑜 d 𝑣 = 𝜌 d 𝜌 d 𝜃 d 𝑧 න 0 ൗ 𝜋 2 = න d 𝜃 0 𝑎 𝑧 d 𝑧 原式 = ʃʃʃΩ z𝜌 2 d 𝜌 𝑑𝜃𝑑𝑧 = 8 9 𝑎 3 柱面 𝜌 = 2 cos 𝜃 成半圆柱体. ʃʃʃΩ 𝑧 𝑥 2 + 𝑦 2 d 𝑥 d 𝑦 d 𝑧