
第十章 重积分
重积分 第十章 重 积 分

第四讲 极坐标系下的二重积分的计算
重积分 第四讲 极坐标系下的二重积分的计算

重积分 1.极坐标下计算二重积分 在极坐标系下,用同心圆r=常数 Q=日+9 及射线0=常数,分划区域D为 0=0k △OK 40k(k=1,2,.n) 0 r=Tk'x 则除包含边界点的小区域外,小区域的面积 w+ara0-宫29s =x+x+ADIAT40 =Tk△rk·△8k k 在△ok内取点T,日),对应有 入 5k Tk cos Ok,nk Tk sin Ok
重积分 1.极坐标下计算二重积分 ᵆ ᵆ ᵅ 对应有 则除包含边界点的小区域外,小区域的面积 ᵮ ᵰ ᵅ = 1 2 [ ᵅ ᵅ + (ᵅ ᵅ + ᵮ ᵅ ᵅ )]ᵮ ᵅ ᵅ ⋅ ᵮ ᵰ ᵅ ᵮ ᵰ ᵅ (ᵅ = 1,2, ⋯ ,ᵅ ) 在 ᵮ ᵰ ᵅ ᵰ = ᵰ ᵅ ᵰ =ᵰ ᵅ +ᵮ ᵰ ᵅ ᵅ = ᵅ ᵅ ᵮ ᵰ ᵅ 内取点 = 1 2 ( ᵅ ᵅ + ᵮ ᵅ ᵅ ) 2 ⋅ ᵮ ᵰ ᵅ ᵅ ᵅ ᵮ ᵅ ᵅ ᵮ ᵰ ᵅ ᵅ ᵅ ᵮ ᵰ ᵅ

重积分 ∑ f(5k,nk)△o =1 ∑f(ncos可s,元sin元4A0k k三1 f.df(rcssim0)rdrdo
重积分 即
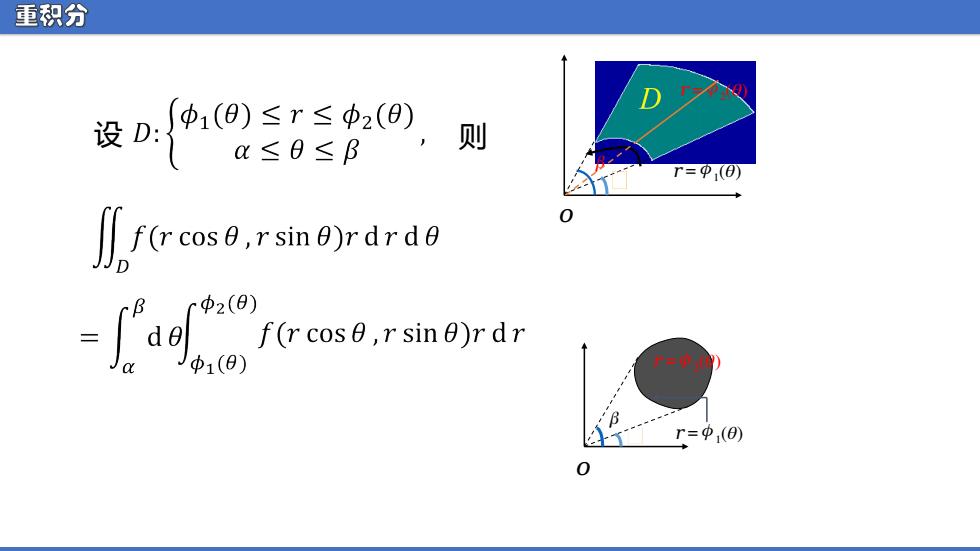
重积分 设-a@ ≤0≤B 则 r=φ,(0) ∥o9,rsin8 rdrdd r中2(8) =ao f(r cose,rsine)rdr 中1(θ) r=φ(0)
重积分 ᵯ ᵅ ᵅ = ᵱ 1 ( ᵰ ) ᵅ = ᵱ 2 ( ᵰ ) ᵅ = ᵱ 1 ( ᵰ ) ᵯ ᵅ ᵅ = ᵱ 2 ( ᵰ ) 设 则