
第二讲 旋转体的体积
定积分及其应用 第二讲 旋转体的体积

定积分及其应用 定积分的应用 1 复习平面图形面积的求法 、 2 定积分在几何上的应用 、 3 定积分在物理上的应用
定积分及其应用 1 复习平面图形面积的求法 、 3 、 定积分在物理上的应用 2 、 定积分在几何上的应用 一、定积分的应用
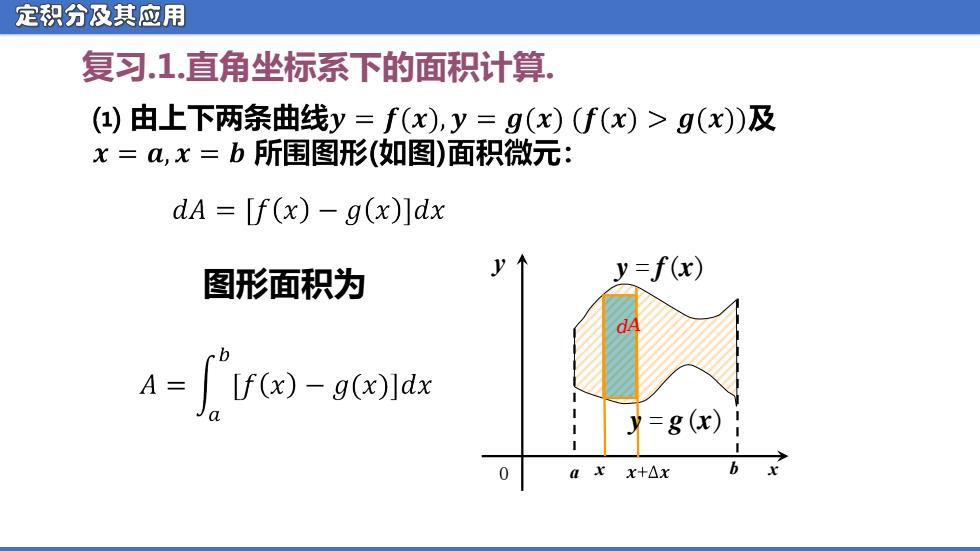
定积分及其应用 复习.1.直角坐标系下的面积计算, (4)由上下两条曲线y=f(x),y=g(x)f(x)>g(x)及 x=a,x=b所围图形(如图)面积微元: dA [f(x)-g(x)]dx 图形面积为 y=f(x) dA A=["If(x)-g(x)]dx =g(x) 0 axx+△x
定积分及其应用 复习.1.直角坐标系下的面积计算. 图形面积为 O ᵉ = ᵈ (ᵉ ) y ᵉ = ᵈ(ᵉ ) a x b x ᵅ ᵃ
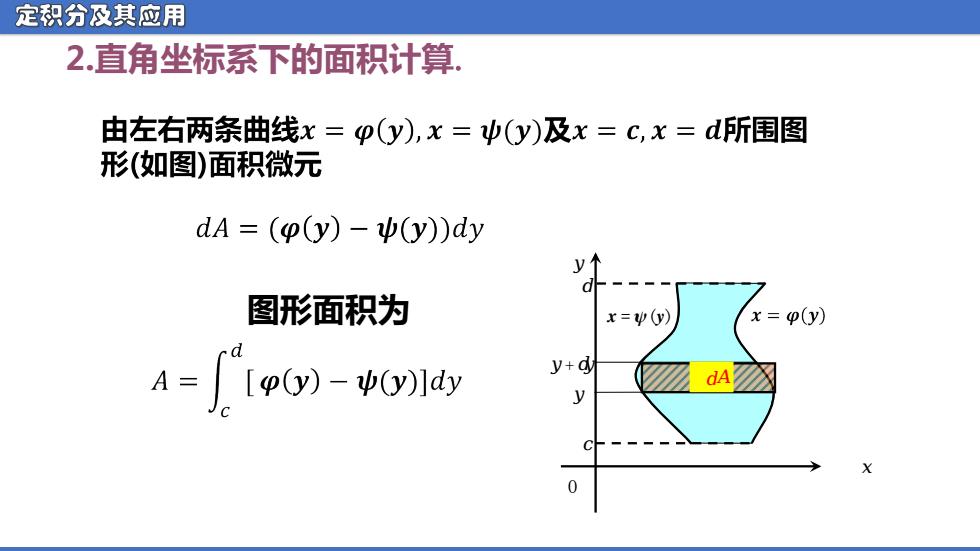
定积分及其应用 2.直角坐标系下的面积计算 由左右两条曲线x=p(y),x=y)及x=c,x=d所围图 形(如图)面积微元 dA=((y)-(y))dy d 图形面积为 x=v(y) X三( e(y) A=Ip)-(y)ldy y+d dA X 0
定积分及其应用 2.直角坐标系下的面积计算. 图形面积为 O ᵆ ᵆ ᵅ ᵆ + ᵅᵆ ᵆ ᵅ ᵉ = ᵴ (ᵉ ) ᵅ ᵃ

定积分及其应用 一、复习引入: 圆柱体体积: r 2 V=πrh 旋转体就是由一个平面图形饶这平面内一条直线旋转一周而成的 立体.这直线叫做旋转轴
定积分及其应用 一、复习引入: 圆柱体体积: ℎ ᵅ 旋转体就是由一个平面图形饶这平面内一条直线旋转一周而成的 立体.这直线叫做旋转轴. ᵄ = ᵰ ᵅ 2 ℎ