
第一讲 主讲人:卢自娟 微分方程的概念
微 分 方 程 第一讲 微分方程的概念 主讲人:卢自娟

微分方程 引例 例1:一条曲线通过点(1,2),且在该曲线上任意一 点M(x,y)处的切线斜率为2x,求这条曲线的方程。 解:设曲线方程为y=f(x), 由题意可知:=2x或dy=2xdx(①, 对(式积分得:y=2xdx=x2+C(I) .曲线过(1,2)点,代入()式得C=1,则得所求曲 线方程为:y=x+1
微 分 方 程 解: 由题意可知: (ᵀᵀ ) ᵈᵉ ᵈᵉ = ᵽ ᵉ ᵉ = ᵉ ᵽ + ᵼ 引例

微分方程 例2:列车在平直线路上以20m/s的速度行驶,当制动时列车 获得加速度-0.4m/s2.求列车制动阶段的运动规律? 解:设求的函数为s=s(t),由题意可知: d2s =-0.4 (I), dt2 对I四式积分得:0.4dt=一0.4t+G1应 对(IV式积分得:s=∫(-0.4t+C1)dt=-0.2t2+C1t+C2(V) 把v(0)=20m/s,s(0)=0,分别代入(IV、(V)得C1=20,C2=0, 则列车制动阶段的运动规律为s=-0.2t2+20t
微 分 方 程 解: 由题意可知: (ᵀᵁ ) (ᵁ )

微分方程 1.微分方程的概念 定义1:含有未知函数的导数(或微分)的方程称 为微分方程。 d2s dy=2xdx(①D, dt2 =-0.4(1I0), 定义2:微分方程中所出现的未知函数的最高阶导数 的阶数,叫作微分方程的阶
微 分 方 程 1. 微分方程的概念 定义1:含有未知函数的导数(或微分)的方程称 为微分方程。 定义2:微分方程中所出现的未知函数的最高阶导数 的阶数,叫作微分方程的阶
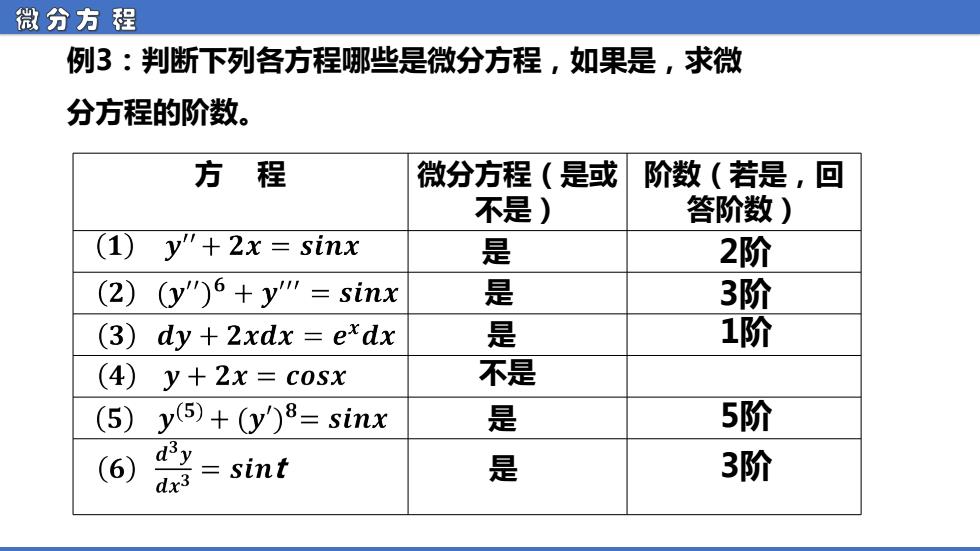
微分方程 例3:判断下列各方程哪些是微分方程,如果是,求微 分方程的阶数。 方程 微分方程(是或 阶数(若是,回 不是) 答阶数) (1)y+2x=sinx 是 2阶 (2) (y")6 +y""=sinx 是 3阶 (3)dy +2xdx exdx 是 1阶 (4) y+2x=cosx 不是 (5) y5)+y)8=sinx 是 5阶 (6) = sint 是 3阶
微 分 方 程 例3:判断下列各方程哪些是微分方程,如果是,求微 分方程的阶数。 方 程 微分方程(是或 不是) 阶数(若是,回 答阶数) 是 2阶 是 是 3阶 1阶 不是 是 5阶 是 3阶