
第二讲 定积分的性质
定积分及其应用 第二讲 定积分的性质

定积分及其应用 定积分的性质 性质1∫f(x)±g(x]dx=f(x)dx±∫g(x)dx 即两个函数和(差)的定积分等于它们定积分的和(差)· n 证:f[fox)±g(x]dx=g∑f)±95]△x 11 =∑r±∑9a=f)t±公g i=1 注 1、 本课程所有性质中研究的函数均为可积函数。 意 2、性质1可以推广到有限多个函数作和的情况
定积分及其应用 性质1 即两个函数和(差)的定积分等于它们定积分的和(差). 证: 注 意 1、本课程所有性质中研究的函数均为可积函数。 2、性质1可以推广到有限多个函数作和的情况。 一. 定积分的性质

定积分及其应用 性质2积分数乘性质 kf(x)dx =kf(x)dx (k为常数) 即被积函数的常数因子可以提到积分号外. ■性质4[积分线性性质] 21dx口的dc口b加a y=1
定积分及其应用 性质2 [积分数乘性质 ] 即被积函数的常数因子可以提到积分号外. 性质4 [积分线性性质] ᵄ ᵄ ᵄ ᵆ ᵆ ᵆ = 1
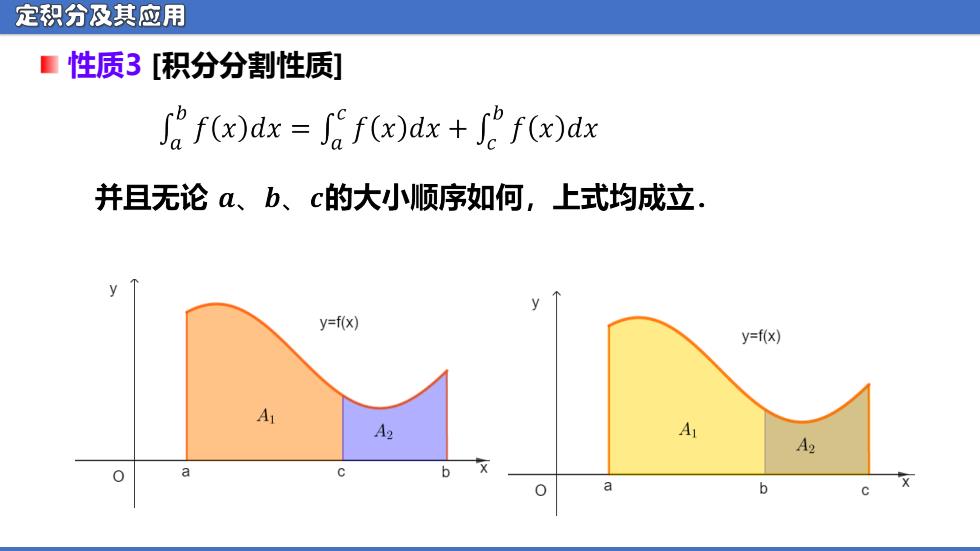
定积分及其应用 ■性质3[积分分割性质] f(x)dx f(x)dx+f(x)dx 并且无论a、b、c的大小顺序如何,上式均成立. y=f(x) y=f(x) A A2 A A2 a b
定积分及其应用 性质3 [积分分割性质]
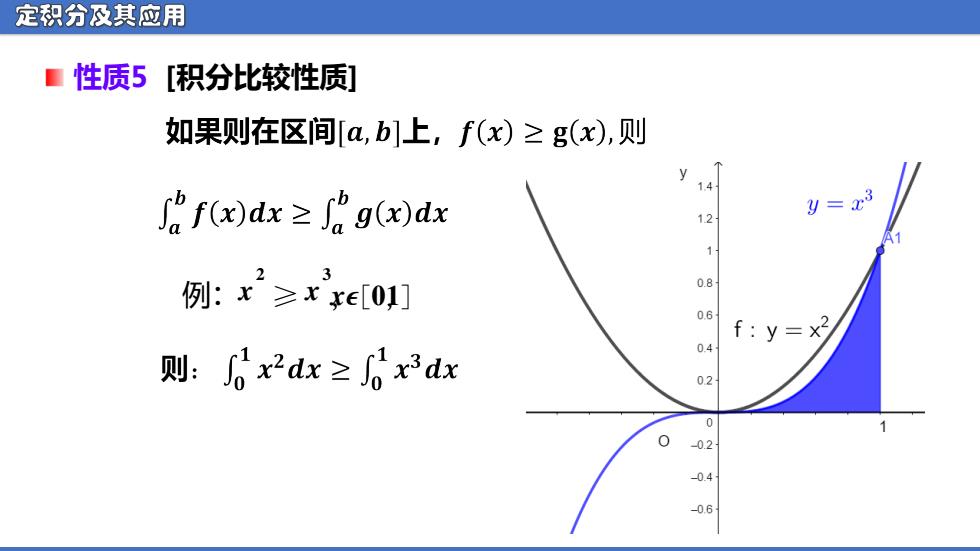
定积分及其应用 ■性质5[积分比较性质] 如果则在区间[a,b]上,f(x)≥g(x),则 2fx)dx≥hgx)dx 12 y=x3 1 例:x≥xxe[0] 08 06 f:y=x2 0.4 则:0x2dx≥0x3dx 02 0.2 -0.4 -0.6
定积分及其应用 性质5 [积分比较性质] 例:ᵉ ᵽ ≥ ᵉ ᵽ ,ᵉ ᵵ [ᵼ ,ᵼ ]