
第二讲 定积分的性质
第二讲 定积分的性质

定积分及其应用 一.定积分的性质 性质1f(x)±g(x]dx=∫f(x)dx±g(x)dx 即两个函数和(差)的定积分等于它们定积分的和(差) 证:Lf()士g(x]ax=∑f5)±gax =r0主sa=7 CirLPny 注 1、 本课程所有性质中研究的函数均为可积函数。 意 2、性质1可以推广到有限多个函数作和的情况
性质1 即两个函数和(差)的定积分等于它们定积分的和(差). 证: 注 意 1、本课程所有性质中研究的函数均为可积函数。 2、性质1可以推广到有限多个函数作和的情况。 一. 定积分的性质 �� 𝑏 �� = �𝑑� �� �� ± �� �� 𝑏 �� ± �𝑑� �� �� 𝑏 𝑔 𝑥 𝑑𝑥 �� 𝑏 𝑓 𝑥 ± 𝑔 𝑥 𝑑𝑥 = 𝑙𝑖𝑚 𝜆→0 𝑖=1 𝑛 [𝑓(𝜉𝑖) ± 𝑔(𝜉𝑖)]∆𝑥𝑖 = 𝑙𝑖𝑚 𝜆→0 𝑖=1 𝑛 𝑓(𝜉𝑖)∆𝑥𝑖 ± 𝑙𝑖𝑚 𝜆→0 𝑖=1 𝑛 �� = �𝑥�∆(�𝜉�)�� 𝑏 �� ± �𝑑� �� �� 𝑏 𝑔 𝑥 𝑑𝑥
定积分及其应用 ■性质2[积分数乘性质] 由kf(x)dx=kj2f(x)dx (k为常数) 即被积函数的常数因子可以提到积分号外. ■性质4[积分线性性质] =1 ∫1c=∫dc=b-. 6
性质2 [积分数乘性质] 即被积函数的常数因子可以提到积分号外. 性质4 [积分线性性质] dx b a 1 dx b a = = b − a. �� 𝑏 �� �� = �𝑑� �� �𝑘� 𝑏 𝑓 𝑥 𝑑𝑥 (𝑘为常数) 𝑎 𝑂 b 𝑥 𝑦 𝑦 = 1
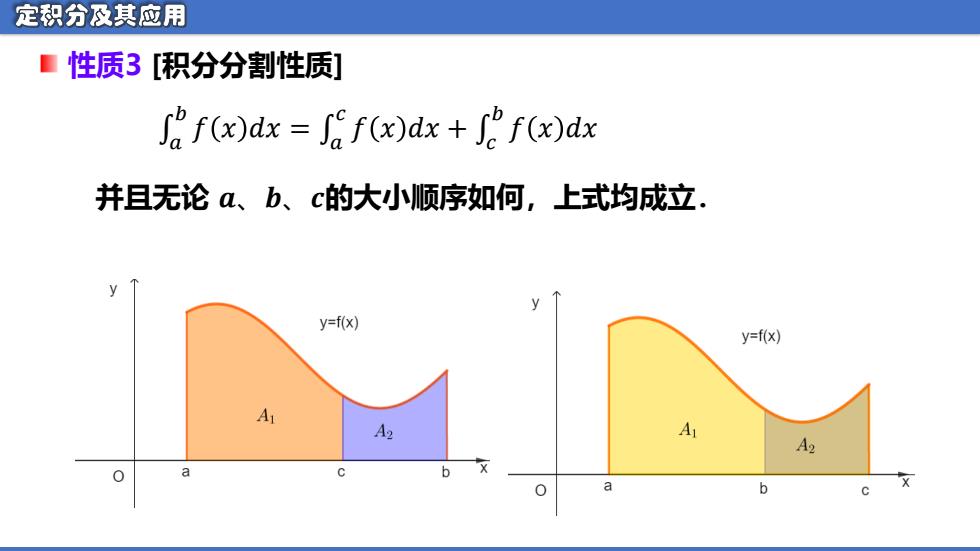
定积分及其应用 ■性质3[积分分割性质] f(x)dx Jf(x)dx+f(x)dx 并且无论a、b、c的大小顺序如何,上式均成立 y=f(x) y=f(x) A A2 A A2 a b
并且无论 𝒂、𝒃、𝒄的大小顺序如何,上式均成立. 性质3 [积分分割性质] �� 𝑏 �� = �𝑑� �� �� 𝑐 �� + �𝑑� �� �� 𝑏 𝑓 𝑥 𝑑𝑥
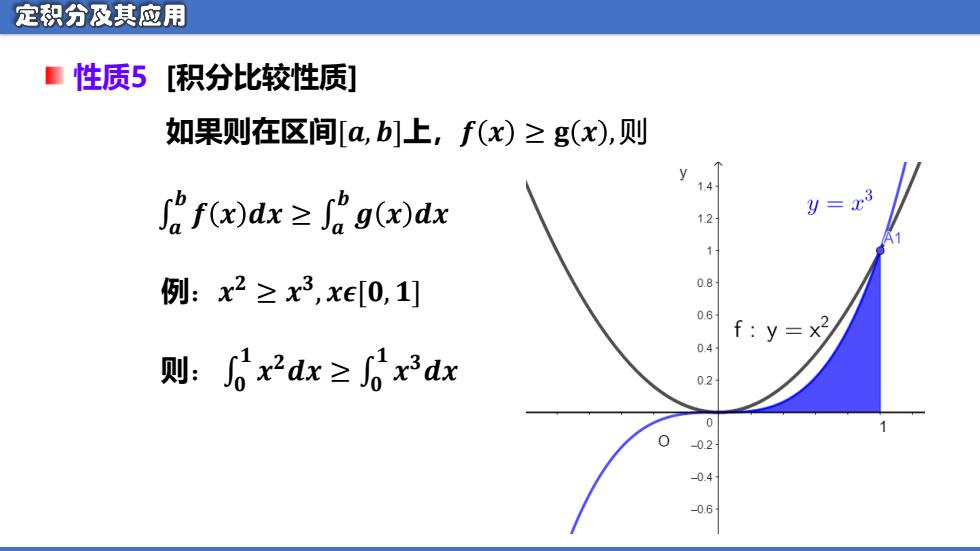
定积分及其应用 ■性质5[积分比较性质] 如果则在区间[a,b]上,f(x)≥g(x),则 af(x)drx≥ag(x)dx 12 y=x3 1 例:x2≥x3,xe[0,1] 08 06 f:y=x2 0.4 则:x2dx≥6xdx 02 02 -0.4 -0.6
性质5 [积分比较性质] 如果则在区间[𝒂, 𝒃]上,𝒇 𝒙 ≥ 𝐠 𝒙 , 则 例:𝒙 𝟐 ≥ 𝒙 𝟑 , 𝒙𝝐[𝟎, 𝟏] �� :则 𝟏 𝒙 �� ≤ �𝒅𝟐� 𝟏 𝒙 𝟑𝒅𝒙 �� 𝒃 �� ≤ �𝒅� �� �� 𝒃 𝒈 𝒙 𝒅𝒙