
第五讲 曲线的凹凸性与拐点
第五讲 曲线的凹凸性与拐点
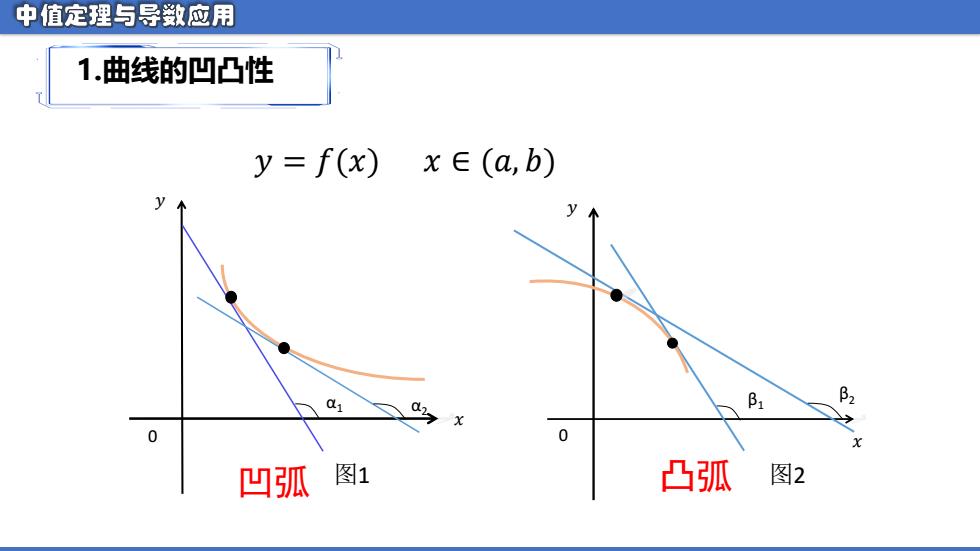
中值定理与导数应用 1.曲线的凹凸性 y=f(x)x∈(a,b) y B2 0 0 凹孤 图1 凸孤 图2
𝑥 𝑥 𝑦 𝑦 0 0 α1 α2 β1 β2 凹弧 图1 凸弧 图2 𝑦 = 𝑓(𝑥) 𝑥 ∈ (𝑎, 𝑏) 1.曲线的凹凸性

中值定理与导敛应用 2.曲线的凹凸性的概念 定义1:在区间(α,b)内,若曲线弧位于其任意一点切 线的上方,则称曲线弧在(α,b)内是凹的(或凹弧), 此区间(a,b)称为凹区间; 若曲线弧位于其任意一点切线的下方,则称曲线弧在 (α,b)内是凸的(或凸弧),此区间(a,b)称为凸区间
定义1:在区间(𝒂, 𝒃)内,若曲线弧位于其任意一点切 线的上方,则称曲线弧在(𝒂, 𝒃)内是凹的(或凹弧), 此区间(𝒂, 𝒃)称为凹区间; 若曲线弧位于其任意一点切线的下方,则称曲线弧在 (𝒂, 𝒃)内是凸的(或凸弧),此区间(𝒂, 𝒃)称为凸区间。 2.曲线的凹凸性的概念
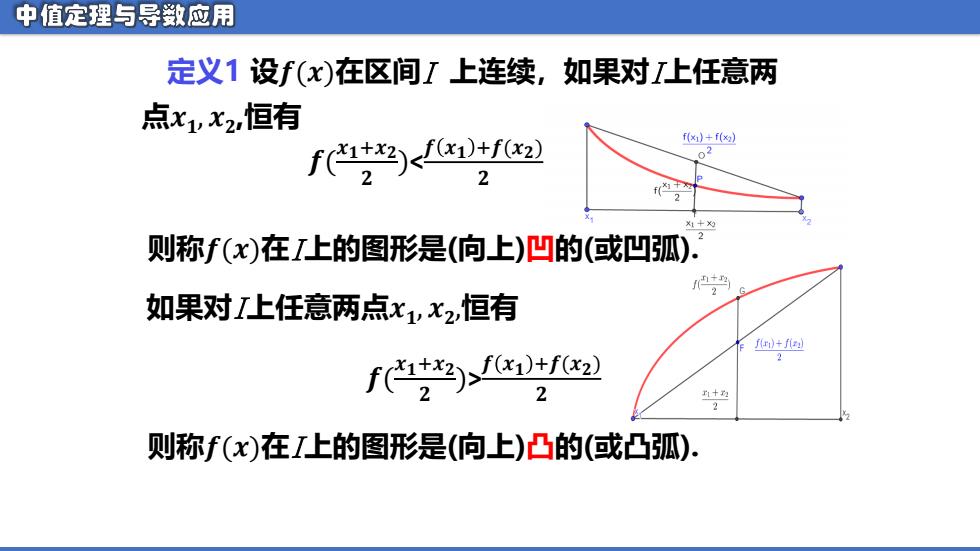
中值定理与导数应用 定义1设f(x)在区间I上连续,如果对上任意两 点x1vx2,恒有 f)+f(x2】 f)xf0 03 2 则称f(x)在I上的图形是(向上)凹的(或凹弧). 如果对I上任意两点x1,x2,恒有 f+f则 2 十边 2 则称f(x)在I上的图形是(向上)凸的(或凸弧)
定义1 设𝒇(𝒙)在区间I 上连续,如果对I上任意两 点𝒙𝟏 , 𝒙𝟐 ,恒有 则称𝒇(𝒙)在I上的图形是(向上)凹的(或凹弧). 如果对I上任意两点𝒙𝟏 , 𝒙𝟐 ,恒有 则称𝒇(𝒙)在I上的图形是(向上)凸的(或凸弧). 𝒇( 𝒙𝟏+𝒙𝟐 𝟐 )< 𝒇 𝒙𝟏 +𝒇(𝒙𝟐) 𝟐 𝒇( 𝒙𝟏+𝒙𝟐 𝟐 )> 𝒇 𝒙𝟏 +𝒇(𝒙𝟐) 𝟐
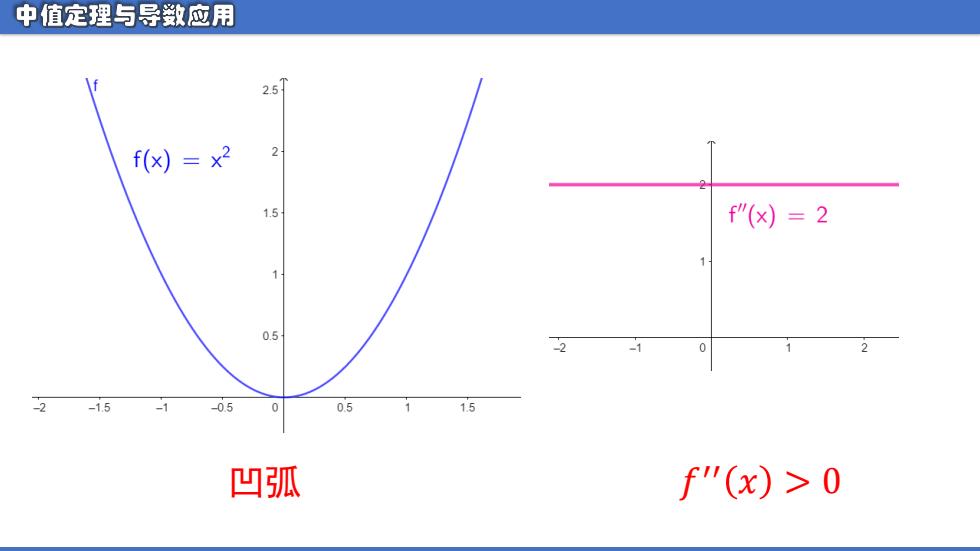
中值定理与导敛应用 257 f(x)=x2 2 1.5 f"(x)=2 1 0.5 -2 -1 0 -1.5 -1 -05 05 1.5 凹孤 f"(x)>0
凹弧 𝑓 ′′ 𝑥 > 0