
第三讲 函数的极值
第三讲 函数的极值
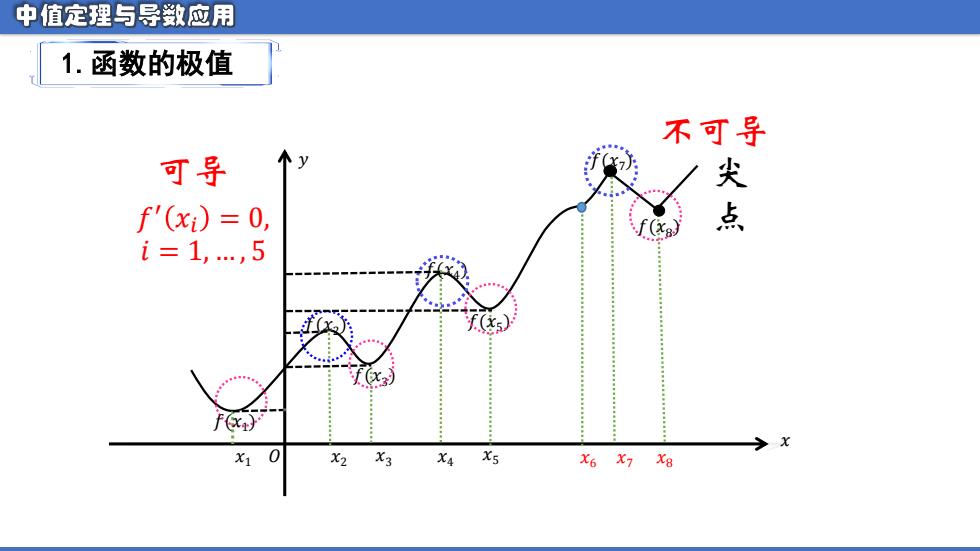
中值定理与导数应用 1.函数的极值 不可导 可导 个y f'(xi)=0, 姿 f(x i=1,.,5 F) x X1 X2 X3 X4 X5 X6 X7 X8
𝑥 𝑦 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑓(𝑥1 ) 𝑓(𝑥2 ) 𝑓(𝑥3 ) 𝑓(𝑥4 ) 𝑓(𝑥5 ) 𝑂 可导 𝑥6 𝑥7 𝑥8 𝑓(𝑥7 ) 𝑓(𝑥8 ) 不可导 尖 点 1.函数的极值 𝑓 ′ 𝑥𝑖 = 0, 𝑖 = 1, . , 5

中值定理与导数应用 2.极值定义 定义1:设函数f(x)在点xo及其近旁有定义,若 对xo近旁任意一点x(x≠xo)均有: (1)f(x)<f(xo),则称f(xo)是f(x)的一个极大值,称点 x,为f(x)的极大值点。 (2)f(x)>f(xo),则称f(x)是f(x)的一个极小值,称点 x,为f(x)的极小值点
定义1:设函数𝒇(𝒙)在点𝒙0及其近旁有定义,若 对𝒙0近旁任意一点𝒙(𝒙 ≠ 𝒙𝟎 )均有: (1) 𝒇(𝒙) < 𝒇(𝒙𝟎 ),则称𝒇(𝒙𝟎 )是𝒇(𝒙)的一个极大值,称点 𝒙𝟎为𝒇(𝒙)的极大值点。 2.极值定义 (2) 𝒇(𝒙) > 𝒇(𝒙𝟎 ),则称𝒇(𝒙𝟎 )是𝒇(𝒙)的一个极小值,称点 𝒙𝟎为𝒇(𝒙)的极小值点

中值定理与导数应用 定义2:函数f(x)的极大值和极小值统称为极值: 极大值点和极小值点统称为极值点。 说明:(1)极值→y,极值点→x. (2)极值局部概念。 (3)极大值不一定比极小值大。 (4)极值点处一定有f'(x)=0或f'(x)不存在
定义2:函数 𝒇(𝒙) 的极大值和极小值统称为极值; 极大值点和极小值点统称为极值点。 说明: (1) 极值→𝒚,极值点→ 𝒙 . (2) 极值局部概念。 (3) 极大值不一定比极小值大。 (4) 极值点处一定有𝒇′(𝒙) = 𝟎或𝒇′(𝒙)不存在

中值定理与导敛应用 定义3:f'(x)=0的实根称为f(x)的驻点。 定理1:如果函数f(x)在x处可导且有极值存在,则f'(xo)=0. 说明:(1)驻点处不一定存在极值。 如y=x3在x=0处不存在极值。 (2)极值一定在f'(x)=0或f'(x)不存在的点处取得。 如y=x在x=0处取得极值
定义3: 𝒇′(𝒙) = 𝟎的实根称为𝒇(𝒙)的驻点。 如果函数𝒇(𝒙)在𝒙𝟎处可导且有极值存在,则𝒇′(𝒙𝟎 定理1: ) = 𝟎 . 说明:(1)驻点处不一定存在极值 。 如𝒚 = 𝒙 𝟑在𝒙 = 𝟎处不存在极值。 (2)极值一定在𝒇′(𝒙) = 𝟎或𝒇′(𝒙) 不存在的点处取得 。 如𝒚 = |𝒙|在𝒙 = 𝟎处取得极值