
第二讲 函数的单调性
第二讲 函数的单调性

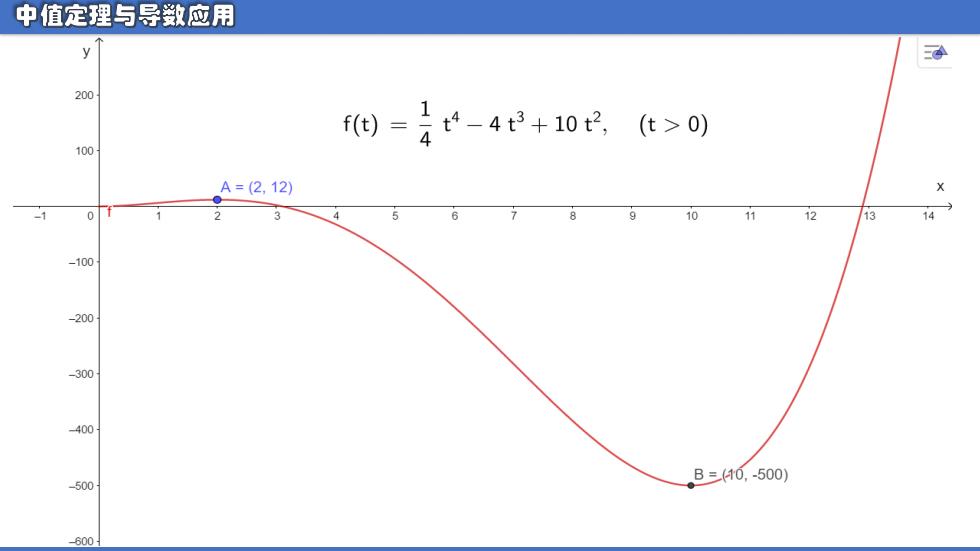
中值定理与导数应用 引例: 设质点作直线运动,其运动规律为: 1 s=44-4t3+102(t>0) (1)何时速度为零? (2)何时作前进运动? (3)何时作后退运动?
引例: 设质点作直线运动,其运动规律为: 𝒔 = 𝟏 𝟒 𝒕 𝟒 − 𝟒𝒕𝟑 + 𝟏𝟎𝒕𝟐(𝒕 > 𝟎) (1)何时速度为零? (2)何时作前进运动? (3)何时作后退运动?
中值定理与导激应用 y 海 200 -4+10民,(t>0 ft)=4 100 A=(2,12) X o f 1 2 3 10 11 2 13 14→ -100 -200 -300 400 B=(40,-500) 500 600
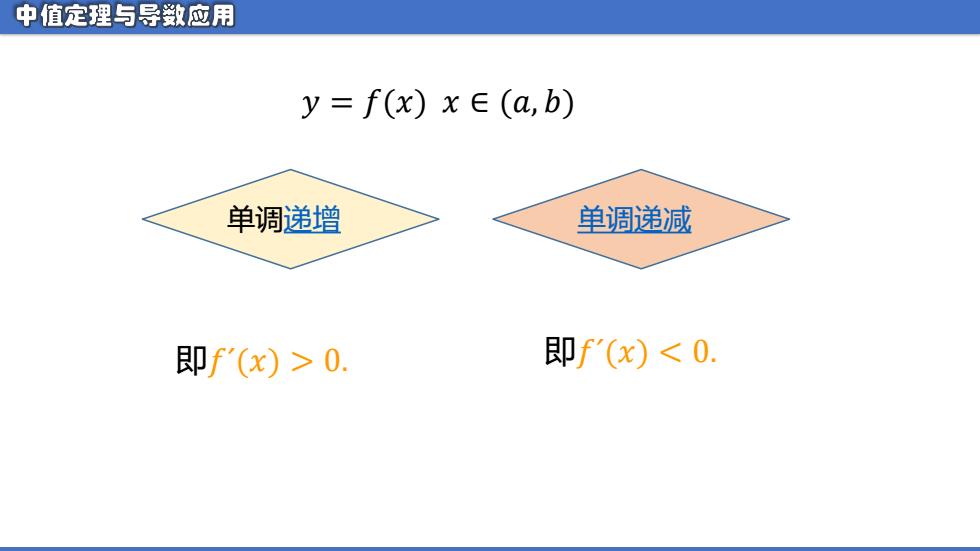
中值定理与导数应用 y=f(x)xE∈(a,b) 单调递增 单调递减 即f'(x)>0. 即f'(x)<0
即𝑓´(𝑥) > 0. 𝑦 = 𝑓(𝑥) 𝑥 ∈ (𝑎, 𝑏) 即𝑓´(𝑥) < 0. 单调递增 单调递减

中值定理与导敛应用 1.函数的单调性 定理1:如果函数f(x): 在[a,b1上连续; 在(a,b)内可导: (1)如果在(a,b)内f'(x)≥0,则f(x)在[a,b]上单调增加。 (2)如果在(a,b)内f'(x)≤0,则f(x)在[ab]上单调减少。 说明:区间可[a,b],(a,b),(a,b],[a,b) 只有有限个点处导数为零
定理1: 如果函数𝒇(𝒙): 在[𝒂, 𝒃]上连续; 在(𝒂, 𝒃)内可导; (1)如果在(𝒂, 𝒃)内𝒇´(𝒙) ≥ 𝟎, 则𝒇(𝒙)在[𝒂, 𝒃]上单调增加。 (2)如果在(𝒂, 𝒃)内𝒇´(𝒙) ≤ 𝟎, 则 𝒇(𝒙) 在 [𝒂, 𝒃] 上单调减少。 说明:区间可[𝒂, 𝒃], (𝒂, 𝒃),(𝒂, 𝒃],[𝒂, 𝒃) 1.函数的单调性 只有有限个点处导数为零