
第二讲 导数的几何意义 可导与连续的关系
第二讲 导数的几何意义 可导与连续的关系
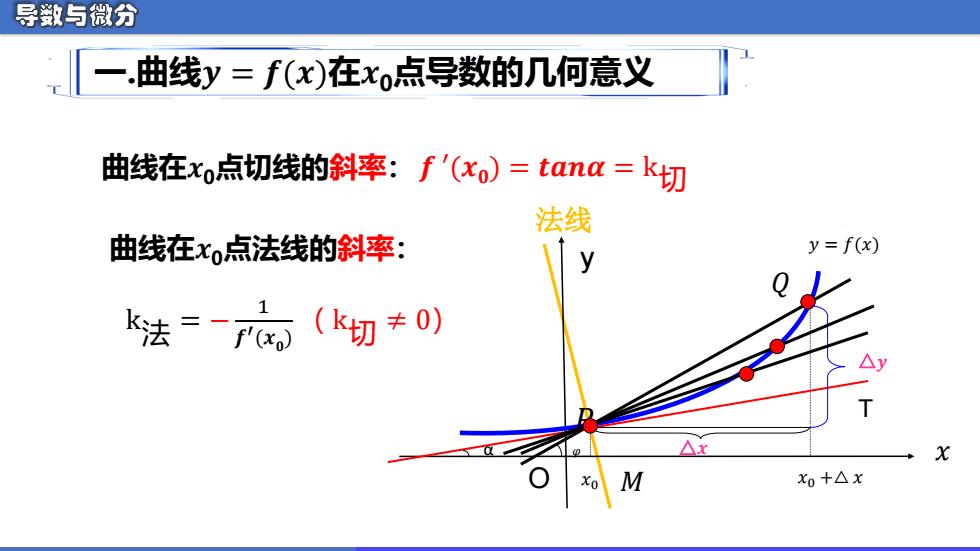
导数与微分 一.曲线y=f(x)在xo点导数的几何意义 曲线在xo点切线的斜率:f'(xo)=tana=k切 法线 曲线在xo点法线的斜率: y=f(x) k法= (k切≠0) X X M x0+△x
曲线在𝒙0点切线的斜率:𝒇 ′(𝒙𝟎 ) = 𝒕𝒂𝒏𝜶 = k切 一 .曲线𝒚 = 𝒇(𝒙)在𝒙0点导数的几何意义 曲线在𝒙0点法线的斜率: k法 = − 1 𝒇 ′(𝒙𝟎 ) ( k切 ≠ 0) 𝑥 y O 𝑥0 𝑥0 +△ 𝑥 𝑦 = 𝑓(𝑥) 𝑃 𝑄 T α 𝜑 △𝒙 △𝒚 法线 𝑀
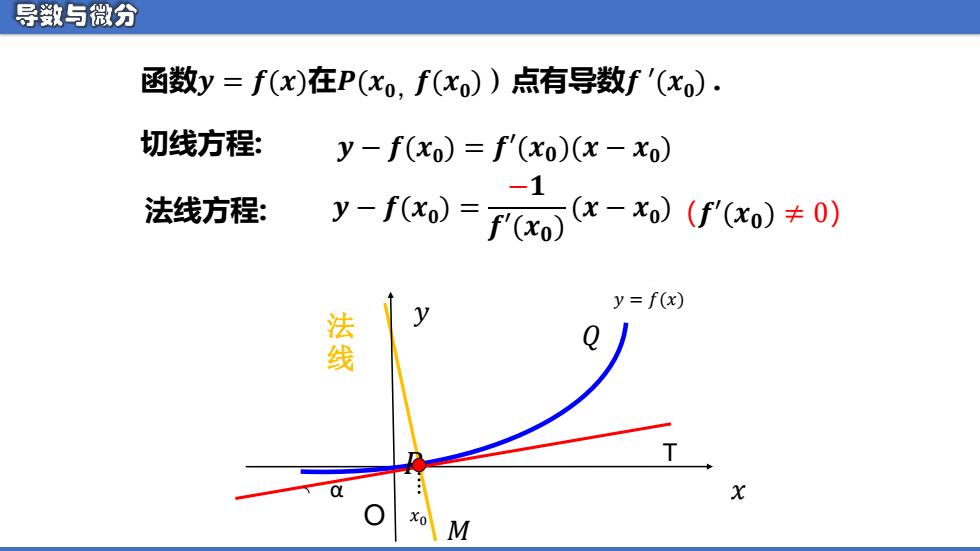
导数与微分 函数y=f(x)在P(xo,f(xo)点有导数f'(xo). 切线方程: y-f(xo)=f(xo)(x-xo) -1 法线方程: y-fxo)=fox-xo)(f'(o)≠0) y=f(x) 线 : X M
函数𝒚 = 𝒇(𝒙)在𝑷(𝒙𝟎,𝒇(𝒙𝟎 ))点有导数𝒇 ′(𝒙𝟎 ) . 切线方程: 法线方程: 𝒚 − 𝒇(𝒙𝟎 ) = −𝟏 𝒇′(𝒙𝟎) (𝒙 − 𝒙𝟎 ) 𝑥 𝑦 O 𝑥0 𝑦 = 𝑓(𝑥) 𝑃 𝑄 T α 法 线 𝑀 𝒚 − 𝒇(𝒙𝟎 ) = 𝒇′(𝒙𝟎)(𝒙 − 𝒙𝟎 ) (𝒇′(𝒙𝟎) ≠ 0)

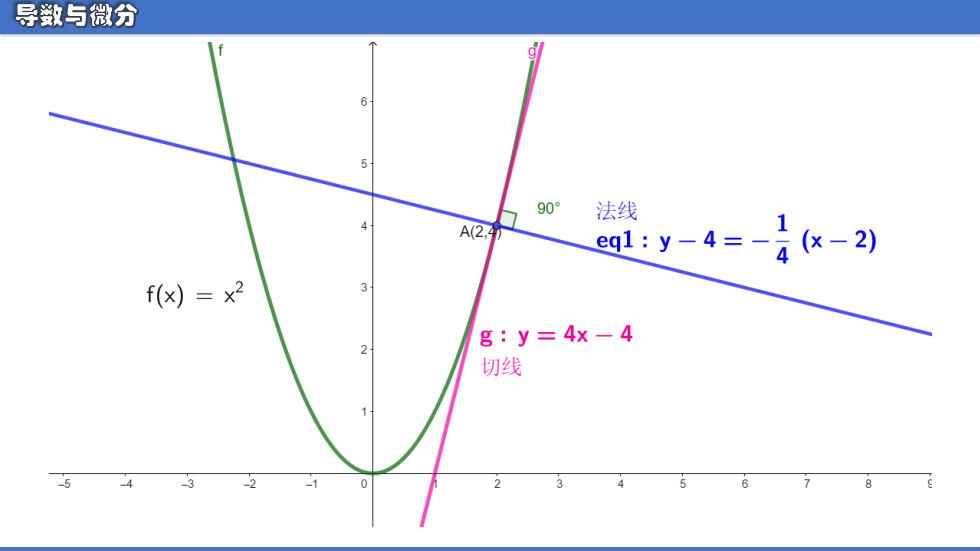
导数与微分 例1:求曲线y=x2在(2,4)处的切线与法线方程。 解: y=(x2)'=2x 求导函数 k=2x|x=2=4=f'(2) 2、求导数值=斜率 切线方程:y-4=4(x-2) 3、写点斜式方程 1 法线方程:y-4=一4x-2) 练习1:求曲线y=x2在(3,9)处的切线法线方程
例1:求曲线𝒚 = 𝒙 2在(2,4)处的切线与法线方程。 解: 𝒚′ = (𝒙 𝟐)′ = 𝟐𝒙 𝒌 = 𝟐𝒙|𝒙=𝟐 = 𝟒 = 𝒇′(𝟐) 切线方程: 𝐲 − 𝟒 = 𝟒(𝒙 − 𝟐) 法线方程: 1、求导函数 2、求导数值=斜率 3、写点斜式方程 𝒚 − 𝟒 = − 𝟏 𝟒 (𝒙 − 𝟐) 练习1:求曲线𝒚 = 𝒙 2在(3,9)处的切线与法线方程
导数与微分 90° 法线 A(2,4 eq1:y-4=- (x-2) f(x)=x2 g:y=4x-4 2 切线 2