
仙 第九讲 两个重要的极限
第九讲 两个重要的极限
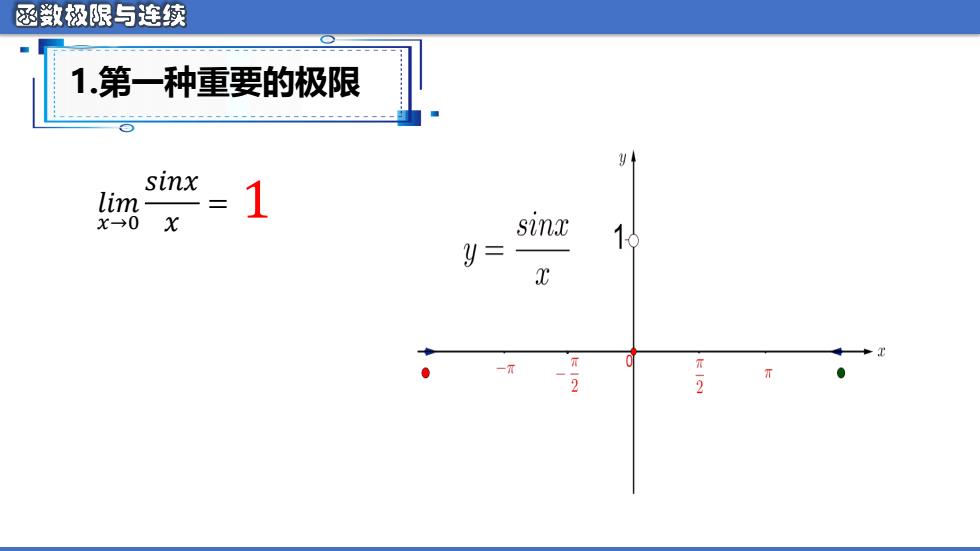
函数极限与连续 1第一种重要的极限 sinx lim 1 X→0 sinx y= 1日 x 2 -2 T
𝑙𝑖𝑚 𝑥→0 𝑠𝑖𝑛𝑥 𝑥 = 1.第一种重要的极限 1
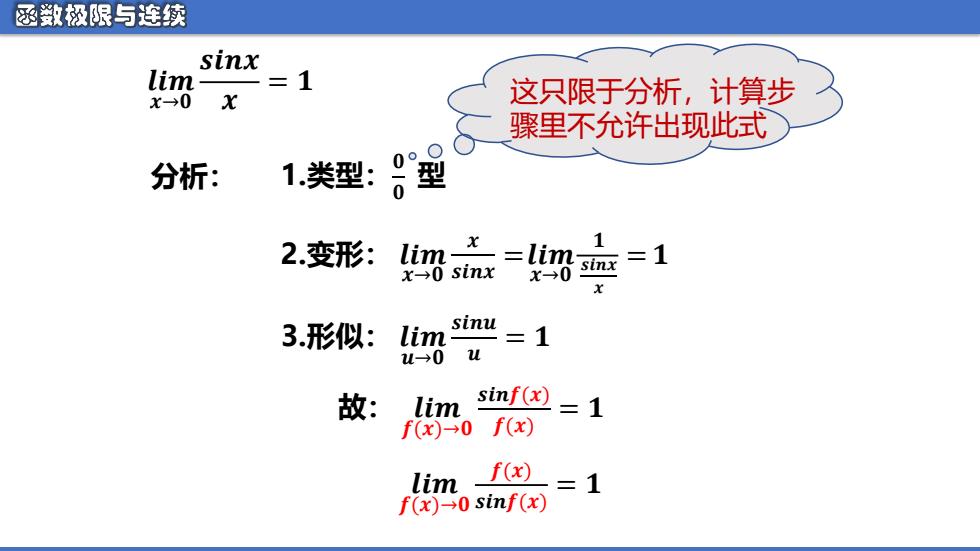
函数极限与连续 inx lim =1 x→0 这只限于分析,计算步 骤里不允许出现此式 ● 分析: 1类型:8型 2.变形: lim父=li 1 =1 x0sinx】 X→0 3形似: lim 二1 sinu u→0 u 故: lim sinf(x)=1 fx)→0f(x) lim f0=1 f(x)→0sinf(x)
分析: 1.类型:𝟎 𝟎 型 2.变形: 𝒍𝒊𝒎 𝒙→𝟎 𝒙 𝒔𝒊𝒏𝒙 = 3.形似: 𝒍𝒊𝒎 𝒖→𝟎 𝒔𝒊𝒏𝒖 𝒖 = 𝟏 故: 𝒍𝒊𝒎 𝒇(𝒙)→𝟎 𝒔𝒊𝒏𝒇(𝒙) 𝒇(𝒙) = 𝟏 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝒙 𝒙 = 𝟏 𝒍𝒊𝒎 𝒙→𝟎 𝟏 𝒔𝒊𝒏𝒙 𝒙 = 𝟏 𝒍𝒊𝒎 𝒇(𝒙)→𝟎 𝒇(𝒙) 𝒔𝒊𝒏𝒇(𝒙) = 𝟏 这只限于分析,计算步 骤里不允许出现此式

函数极限与连续 例1:求下列函数的极限。 (1)lim sin2x ◆分母x→0,分子sin2x→0 →0 解:原式=lim sin2x ×2 X→0 2x sin2x 2×lim X→0台2x→0 2x→0 2x u 2x 2lim u sinu=2x1=2 u-→0
例1: 求下列函数的极限。 (1) 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝒙 解:原式= 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 = 2× 𝒍𝒊𝒎 𝟐𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 = 2𝒍𝒊𝒎 𝒖→𝟎 𝒔𝒊𝒏𝒖 𝒖 = 𝟐ⅹ1=2 𝒖 = 𝟐𝒙 分母𝑥 → 0, 分子𝑠𝑖𝑛 2𝑥 → 0 ×2 𝑥 → 0 ⇔ 2𝑥 → 0

函数极限与连续 (2)lim-i x-0 sin3x 解:原式=lim 3X1 x→0sin3x3 1 ×lim 3x 3 3x→0sin3x X→0台3X→0 u 3x = 久2 u u→0sinu ×1=
(2) 𝒍𝒊𝒎 𝒙→𝟎 𝒙 𝒔𝒊𝒏𝟑𝒙 解:原式= 𝒍𝒊𝒎 𝒙→𝟎 𝟑𝒙 𝒔𝒊𝒏𝟑𝒙 = 𝟏 𝟑 × 𝒍𝒊𝒎 𝟑𝒙→𝟎 𝟑𝒙 𝒔𝒊𝒏𝟑𝒙 = 𝟏 𝟑 ×1= 𝟏 𝟑 = 𝟏 𝟑 × 𝒍𝒊𝒎 𝒖→𝟎 𝒖 𝒔𝒊𝒏𝒖 𝒖 = 𝟑𝒙 × 𝟏 𝟑 𝑥 → 0 ⇔ 3𝑥 → 0