
第十讲 两个重要的极限
第十讲 两个重要的极限
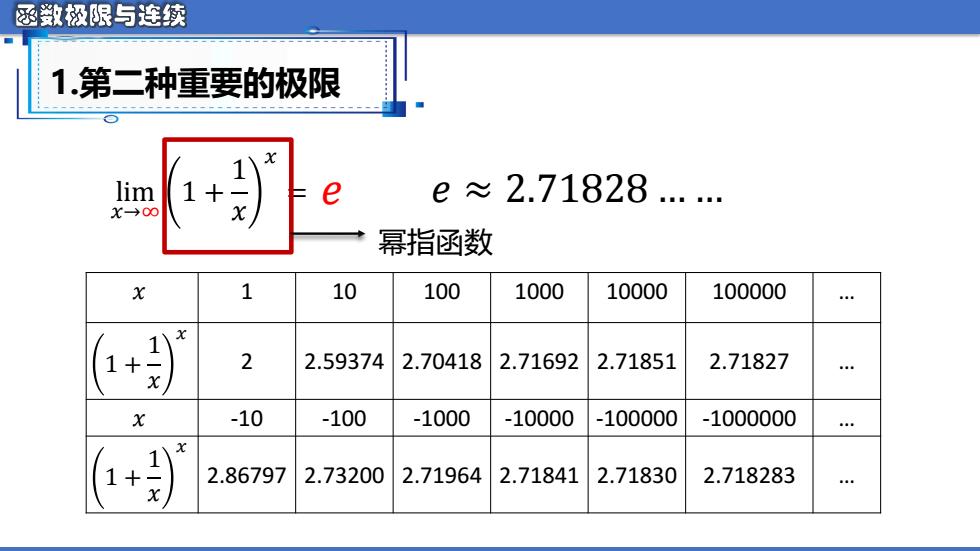
函数极限与连续 1第二种重要的极限 lim + e e≈2.71828. 幂指函数 1 10 100 1000 10000 100000 1+》 2 2.59374 2.70418 2.71692 2.71851 2.71827 X -10 -100 -1000 -10000 -100000 -1000000 2.86797 2.73200 2.71964 2.71841 2.71830 2.718283
lim 𝑥→∞ 1 + 1 𝑥 𝑥 = 𝑒 𝑒 ≈ 2.71828 . . 1.第二种重要的极限 𝑥 1 10 100 1000 10000 100000 . 1 + 1 𝑥 𝑥 2 2.59374 2.70418 2.71692 2.71851 2.71827 . 𝑥 -10 -100 -1000 -10000 -100000 -1000000 . 1 + 1 𝑥 𝑥 2.86797 2.73200 2.71964 2.71841 2.71830 2.718283 . 幂指函数

函数极限与连续 (1+=e 这只限于分析,计算步 分析: 1、类型:1型d 骤里不允许出现此式 2、形似: lm(1+)“=e 1100 ]-e f(x)→0∞ 加号 互为 倒数
分析: 1、类型:𝟏 ∞型 2、形似: 𝒍𝒊𝒎 𝒖→∞ 𝟏 + 𝟏 𝒖 𝒖 = 𝒆 故: 𝒍𝒊𝒎 𝒇(𝒙)→∞ (𝟏 + 𝟏 𝒇(𝒙) ) 𝒇 𝒙 = 𝒆 这只限于分析,计算步 骤里不允许出现此式 𝒍𝒊𝒎 𝒙→∞ 𝟏 + 𝟏 𝒙 𝒙 = 𝒆 加号 互为 倒数
函数极限与连续 例1:求下列函数的极限。 ()lim(1+3x 互为倒数 解:原式=m(1+凰2x一台兰m台kxk+0)一o r00 =m(1+32 u克 =[(1+12 =e2
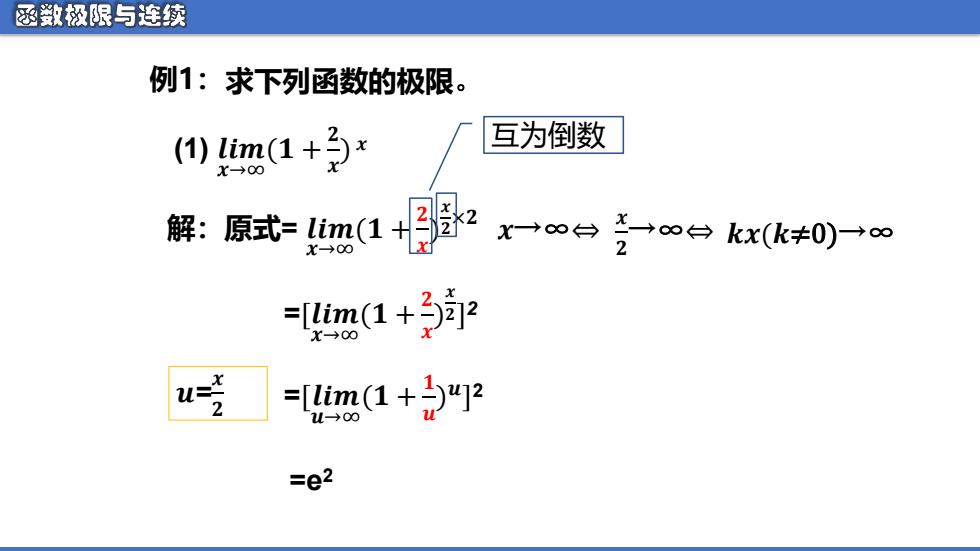
例1:求下列函数的极限。 (1) 𝒍𝒊𝒎 𝒙→∞ (𝟏 + 𝟐 𝒙 ) 𝒙 解:原式= 𝒍𝒊𝒎 𝒙→∞ (𝟏 + 𝟐 𝒙 ) 𝒙 𝟐 ×𝟐 𝒙→∞⇔ 𝒙 𝟐 →∞⇔ 𝒌𝒙(𝒌≠0)→∞ =[𝒍𝒊𝒎 𝒙→∞ (𝟏 + 𝟐 𝒙 ) 𝒙 𝟐] 2 𝒖= 𝒙 𝟐 =[𝒍𝒊𝒎 𝒖→∞ (𝟏 + 𝟏 𝒖 ) 𝒖 ] 2 =e2 互为倒数
函数极限与连续 2lm((1-3 -0o 解原武1F号永 X→00 加号 互为倒数 =m1+子可-2 =e-2
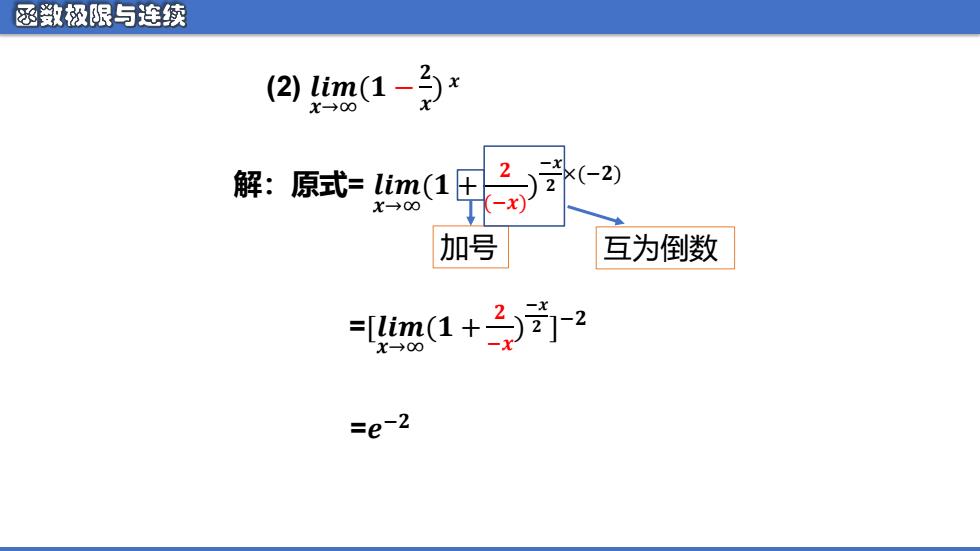
(2) 𝒍𝒊𝒎 𝒙→∞ (𝟏 − 𝟐 𝒙 ) 𝒙 解:原式= 𝒍𝒊𝒎 𝒙→∞ (𝟏 + 𝟐 (−𝒙) ) −𝒙 𝟐 ×(−𝟐) =[𝒍𝒊𝒎 𝒙→∞ (𝟏 + 𝟐 −𝒙 ) −𝒙 𝟐 ] −𝟐 =𝒆 −𝟐 加号 互为倒数