
导数与微分 复习: sinx sin2 (1)1im A:1 B:2 C:0 D: x→2 x2 4 sinx sin2 (2)lim A:1 B:2 C:0 D: X→0 4 sinx sin2 (3)lim 二 A:1 B:2 C:0 D: X→00 x 4 (④)f)=在x=0是 A:第一类间断点B:第二类间断点C:第三类间断点D:连续点 (5)f(x)=n在x=2,是 A:第一类间断点B:第二类间断点C:第三类间断点D:连续点
复习: (𝟏) 𝐥𝐢𝐦 𝒙→𝟐 𝒔𝒊𝒏𝒙 𝒙 𝟐 = 𝑨: 𝟏 𝑩: 𝟐 𝑪: 𝟎 𝑫: 𝒔𝒊𝒏𝟐 𝟒 (𝟐) 𝐥𝐢𝐦 𝒙→𝟎 𝒔𝒊𝒏𝒙 𝒙 = 𝑨: 𝟏 𝑩: 𝟐 𝑪: 𝟎 𝑫: 𝒔𝒊𝒏𝟐 𝟒 (𝟑) 𝐥𝐢𝐦 𝒙→∞ 𝒔𝒊𝒏𝒙 𝒙 = 𝑨: 𝟏 𝑩: 𝟐 𝑪: 𝟎 𝑫: 𝒔𝒊𝒏𝟐 𝟒 𝟒 𝒇 𝒙 = 𝒔𝒊𝒏𝒙 𝒙 在𝒙 = 𝟎,是 𝑨:第一类间断点 𝑩:第二类间断点 𝑪: 第三类间断点 𝑫:连续点 𝟓 𝒇 𝒙 = 𝒔𝒊𝒏𝒙 𝒙 在𝒙 = 𝟐,是 𝑨:第一类间断点 𝑩:第二类间断点 𝑪: 第三类间断点 𝑫:连续点

第一讲 导数概念
第一讲 导数概念

导数与微分 两个引例 1、变速直线运动的瞬时速度 2、平面曲线的切线斜率
两个引例 1、变速直线运动的瞬时速度 2、平面曲线的切线斜率

导数与微分 例1:设某物体作变速直线运动,在[0,t]内所走过 的路程s=s(t)(t>0),求物体在时刻to时的瞬时速度。 解:<1>平均速度 s(to)s(t+△t) 匀 S 人一一t V= 0 to to+△t △s=s(to+△t)-S(to) <2>l△t很小,在[to,to+△t]上 物体的运动近似看作匀速直线运动。 精 <3>取极限,lim △S v(to) △→0△t
例1:设某物体作变速直线运动,在[𝟎, 𝒕]内所走过 的路程𝒔 = 𝒔(𝒕)(𝒕 > 𝟎),求物体在时刻𝒕𝟎时的瞬时速度。 解: t 0 𝑡0 𝑡0 +△t 𝑠(𝑡0 ) 𝑠(𝑡0 +△ 𝑡) △ 𝒔 = 𝒔(𝒕𝟎 +△ 𝒕) − 𝒔(𝒕𝟎 ) <1>平均速度 v = s t <2>|△ 𝒕|很小,在[𝒕𝟎 , 𝒕𝟎 +△ 𝒕]上, 物体的运动近似看作匀速直线运动。 <3>取极限, 0 lim t s t → = 𝒗(𝒕𝟎 精 ) 匀
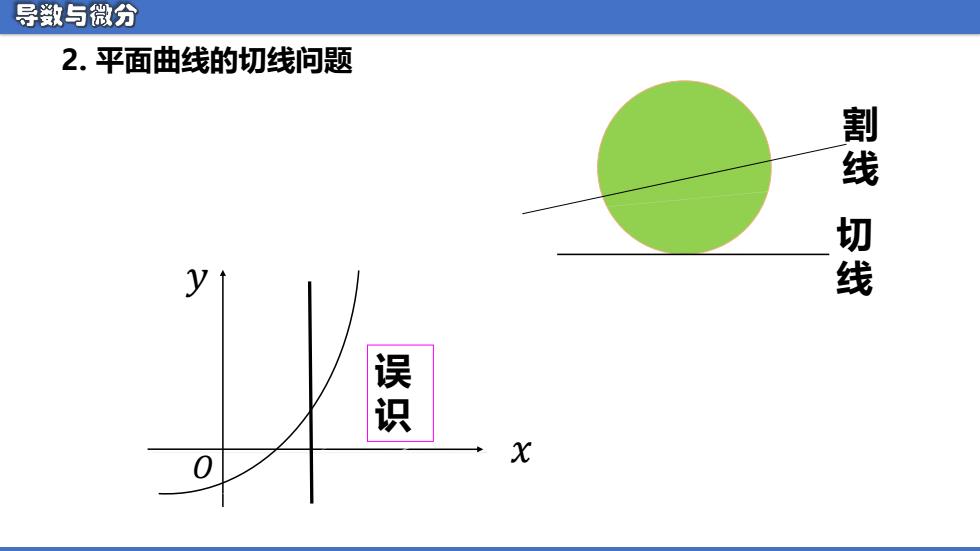
导数与微分 2.平面曲线的切线问题 割线 切线 瀑 X
2. 平面曲线的切线问题 切线割线 𝑥 𝑦𝑂 误识