
第九讲 微分概念
第九讲 微 分 概 念

导数与微分 一微分概念 1.两个引例 2.微分概念 3.微分的几何意义 4.求微分计算
1. 两个引例 2. 微分概念 3. 微分的几何意义 4. 求微分计算 一.微分概念

导数与微分 两个引例 1.正方形金属薄片受热膨胀时面积变化问题 2.自由落体运动的路程问题
两个引例 1. 正方形金属薄片受热膨胀时面积变化问题 2. 自由落体运动的路程问题
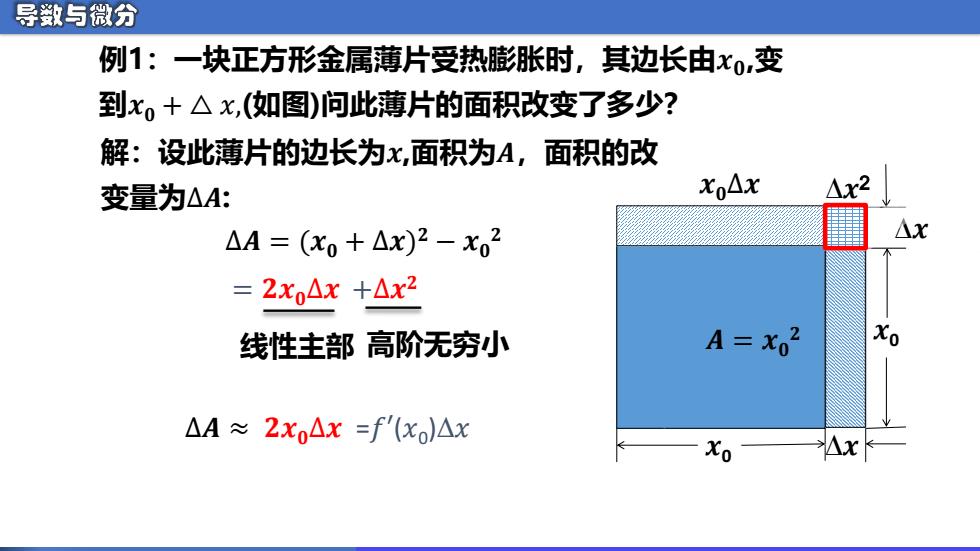
导数与微分 例1:一块正方形金属薄片受热膨胀时,其边长由xo,变 到xo+△x,(如图)问此薄片的面积改变了多少? 解:设此薄片的边长为x,面积为A,面积的改 变量为△A: xo△x 1x2 △A=(x0+△x)2-x2 =2x0△x+△x2 线性主部高阶无穷小 A=x02 △A≈2x△x=f'(xO)△x Xo Ax
例1:一块正方形金属薄片受热膨胀时,其边长由𝒙𝟎,变 到𝒙𝟎 + △ 𝑥,(如图)问此薄片的面积改变了多少? 解:设此薄片的边长为𝒙,面积为𝑨,面积的改 变量为∆𝑨: ∆𝑨 ≈ 𝟐𝒙𝟎∆𝒙 𝒙0 ∆𝒙 𝒙0 ∆𝒙 𝑨 = 𝒙𝟎 𝟐 𝒙𝟎∆𝒙 ∆𝒙 2 ∆𝑨 = (𝒙𝟎 + ∆𝒙) 𝟐 − 𝒙𝟎 𝟐 = 𝟐𝒙𝟎∆𝒙 +∆𝒙 𝟐 线性主部 高阶无穷小 =𝑓′(𝑥0 )∆𝑥

导数与微分 例2:求自由落体由时刻t到t+△t所经过路程的近似值。 解:设自由落体运动的路程为 s=9t2在[t,t+△t]时间 1 S(t) 段内经过的路程为△S: 1 △s=29(t+△t)2 1 9t2 S(t+△t) 业 t+△t =gt△t 29(4)2 线性主部 高阶无穷小 △S≈gt△t=S'(t)△t
例2:求自由落体由时刻𝒕到𝒕 + ∆𝒕所经过路程的近似值。 解: ∆𝑺 ≈ 𝒈𝒕∆𝒕 = 𝒈𝒕∆𝒕 线性主部 高阶无穷小 =𝑺 ′(𝒕)∆𝒕 𝒕 + ∆𝒕 𝑺(𝒕) 𝑺(𝒕 + ∆𝒕) 𝒕 设自由落体运动的路程为 𝒔 = 𝟏 𝟐 𝒈𝒕 𝟐 ,在[𝒕, 𝒕 + ∆𝒕]时间 段内经过的路程为∆𝒔: ∆𝒔 = 𝟏 𝟐 𝒈(𝒕 + ∆𝒕) 𝟐 − 𝟏 𝟐 𝒈𝒕 𝟐 + 𝟏 𝟐 𝒈(∆𝐭) 𝟐