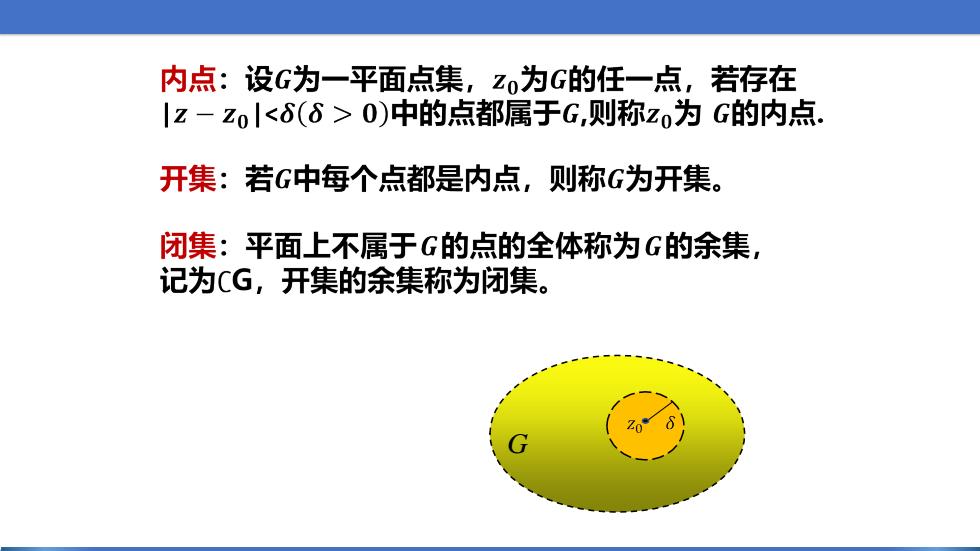
内点:设G为一平面点集,Z为G的任一点,若存在 |z-z0|<6(6>0)中的点都属于G,则称z0为G的内点. 开集:若G中每个点都是内点,则称G为开集。 闭集:平面上不属于G的点的全体称为G的余集, 记为CG,开集的余集称为闭集
ᵃ
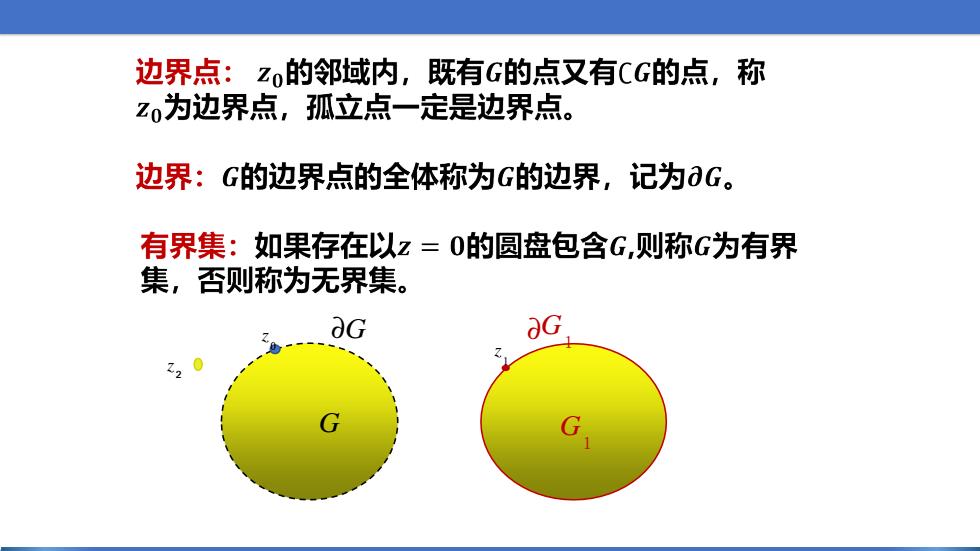
边界点:Zo的邻域内,既有G的点又有CG的点,称 z0为边界点,孤立点一定是边界点。 边界:G的边界点的全体称为G的边界,记为∂G。 有界集:如果存在以z=0的圆盘包含G,则称G为有界 集,否则称为无界集。 OG 22
ᵃ 1 ᵱ ᵃ ᵃ ᵱ ᵃ 1 ᵆ 0 ᵆ 1 ᵆ 2