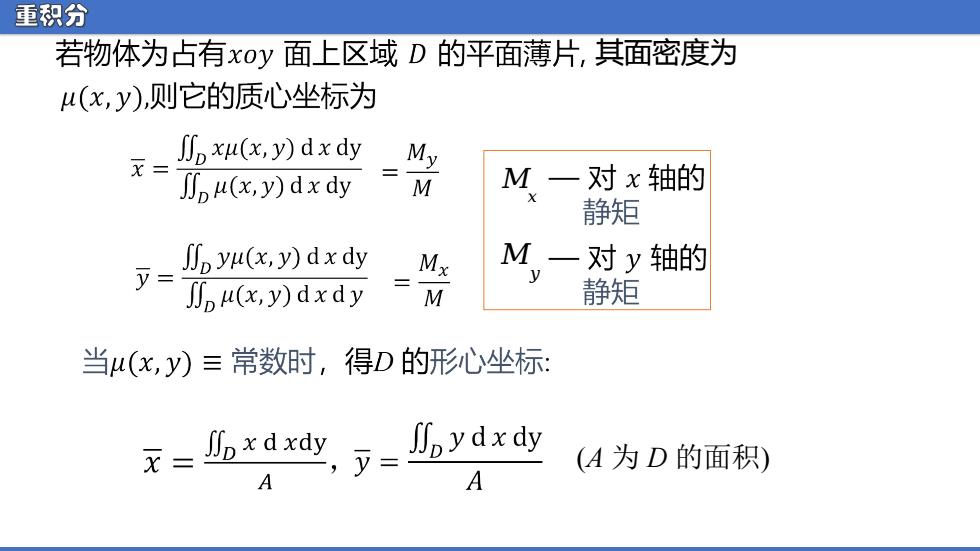
重积分 若物体为占有xoy面上区域D的平面薄片,其面密度为 (x,y),则它的质心坐标为 旷px(x,y)dxdy x= My (y)dx dy M M一对x轴的 静矩 y= yu(xy)dx dy Mx M一对y轴的 u(xy)dxdy M 静矩 当(x,y)三常数时,得D的形心坐标: 元=xdy,y=ydxdy (A为D的面积) A
重积分 其面密度为 ᵄ ᵆ ᵄ ᵆ (A 为 D 的面积)

重积分 例1.求位于两圆r=2sin8和r=4sin0之间均匀薄片 的质心 解:利用对称性可知x=0 而-儿ydxy esinedrde X 4 sin 0 sin 0 d0 3πJ0 r2dr 56 9元J0 sin 0 do J2 sin 0 56 56 .2 sin40d0= 3 1 9n 9元 242
重积分 4 的质心. 而 2 ᵃ = 7 3 之间均匀薄片 3 4 ⋅ 1 2 ⋅ ᵰ 2 ᵅ ᵆ ᵆ ᵃ