
重积分 例1.比较下列积分的大小 c+y2da,∬cx+da 其中D:(x-2)+y-1)≤2 解:积分域D的边界为圆周 X (x-2)+y-1)=2 X+y=1 它与x轴交于点(1,0)与直线x+y=1相切, 而域D位 于直线的上方,故在D上x+y≥1,从而 (x+y)≤(x+y +da5f+ydo
重积分 例1. 比较下列积分的大小: 其中 ᵃ : (ᵆ − 2) 2 + (ᵆ − 1) 2 ≤ 2 解: 积分域 D 的边界为圆周 (ᵆ + ᵆ ) 2 ≤ (ᵆ + ᵆ ) 3 (ᵆ − 2) 2 + (ᵆ − 1) 2 = 2 它与 x 轴交于点 (1,0) , 与直线ᵆ + ᵆ = 1 相切, 而域 D 位 于直线的上方, 故在 D 上 ᵆ + ᵆ ≥ 1, 从而 ᵆ + ᵆ = 1 ᵆ ᵅ 2 ᵆ ᵃ
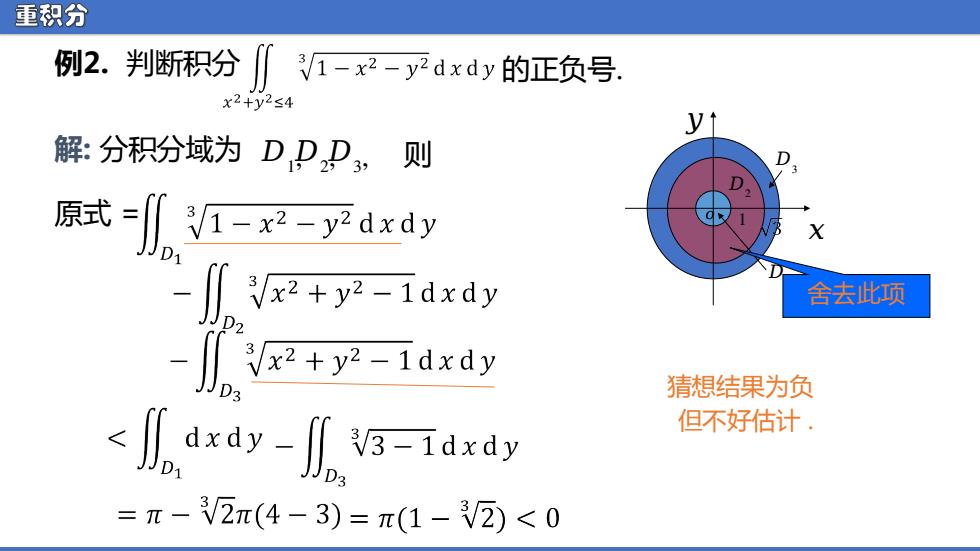
重积分 例2.判断积分 1-x2-y2dxdy的正负号. x2+y2≤4 解:分积分域为DDD, 则 原武=1-2-ydxdy y-1dxdy 舍去此项 -x+y2-idxdy 猜想结果为负 axay- 但不好估计. V3-1dxdy =π-2π(4-3)=π(1-V2)<0
重积分 例2. 判断积分 的正负号. 解: 分积分域为 ᵃ 1 , ᵃ 2 , ᵃ 3 , 则 原式 = ᵃ 3 ᵃ 2 1 ᵃ 1 ᵆ ᵆ ᵅ 猜想结果为负 但不好估计 . 舍去此项