《线性代数》课程PPT教学课件（同济第五版）第三章 矩阵的初等变换与线性方程组 第三节 线性方程组的解

其中x,+1,.xn为自由未知数说明为什公) 而称1，飞，为基本未知数， 现令自由未知数1=G1,xn=c-,即得方程) 的含n-r参数的解 -b.c-.-bc+d -b.c.-.-b c +d

的含n − r参数的解 , , r 1 1 n n r x c x c 现令自由未知数+ =  = − 其中xr+1 , xn 为自由未知数。 而称x1 ,  , xr 为基本未知数，(说明为什么?) 即得方程(4)                     + n r r x x x x   1 1                     − − − + − − − + = − − − − − n r r r n r n r r n r n r c c b c b c d b c b c d     1 1 1 , 1 1 1 1 , 1

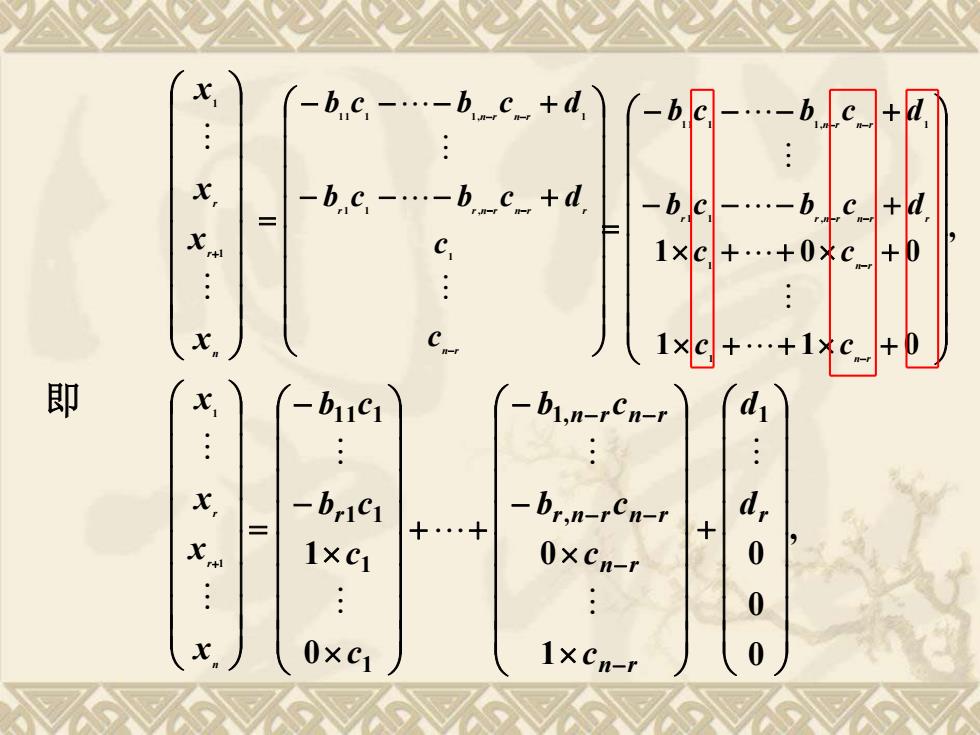
-bc-.-bc+d -b.c. - b.c +a -b.c-.-b.c+d -bc -.-b,c+d 1xc+.+0Xc+0 1×c+.+1c+0 即 -b11C1 -b,n-rcn-r .: . -b1C1 十.十 -brin-rCn-r 1×C1 0×Cn-r 0 0 0×c1 1×Cn-r 0

                    + n r r x x x x   1 1                     − − − + − − − + = − − − − − n r r r n r n r r n r n r c c b c b c d b c b c d     1 1 1 , 1 1 1 1 , 1 即                     + n r r x x x x   1 1 0 1 1 1 1 1 11 1                       − − = c c b c b c r   , 1 1 0 1 0 0 1 1 1 1 , 1 1 1 1, 1                      + +  +  + +  + − − − + − − − + = − − − − − − n r n r r r n r n r r n r n r c c c c b c b c d b c b c d       1 0 , 1,                       − − + + − − − − − − n r n r r n r n r n r n r c c b c b c    , 0 0 0 1                     + dr d 

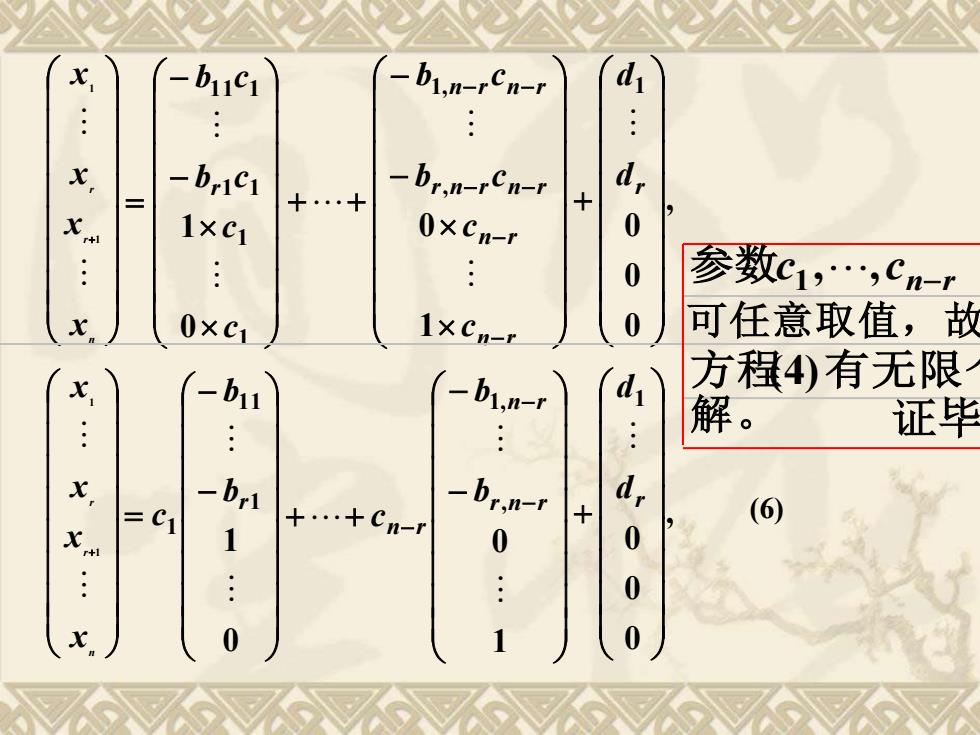
-b11C1 bi.n-rCn-r d : : t -b1C1 +十 -br:n-rCn-r + % 1×C1 0xCn-r 0 : 0 参数C1,Cn-r 0×c1 1×Cm-r 0 可任意取值，故 -b11 -bi,n-r 方程4)有无限 .· : 解 证毕 -br =C1 1 +.+Cn- -br.n-r (6) r+1 0 000

                    + n r r x x x x   1 1 0 1 1 1 1 1 11 1                       − − = c c b c b c r   1 0 , 1,                       − − + + − − − − − − n r n r r n r n r n r n r c c b c b c    , 0 0 0 1                     + dr d                      + n r r x x x x   1 1 0 1 1 11 1                     − − =   br b c 1 0 , 1,                     − − + + − − −    r n r n r n r b b c , 0 0 0 1                     + dr d  n r c c − , , 参数 1  可任意取值，故方 方程(4) 有无限个 解。 证毕 (6)

当R(A)=R(A)=r<时由于-r个参数的辋 可表示线程组5)的任一队而他可表示线性方程 组3)的任一图此解6)称为线性方程的通解 定理3的证明过程也蹄了求解线性方程组的 组的访法和步骤现将它归纳如下： (1)对于非齐次线性程组， 作行变换 增广矩阵B行阶梯形矩阵， 同时看出R(A)和R(B): 若R(A)≠R(B),(只能R(A)<R(B)则方程组无解 若R(A)=R(B),继续下一步

当R ( A ) = R ( A ) = r  n时 ， 方程组(5)的任一解， 因此解(6)称为线性方程组(3）的通解. 定 理3的证明过程也给出了求解线性方程组的方 现将它归纳如下： ⑴ 对于非齐次线性方程 组 ， 增广矩阵B ～ r 行阶梯形矩阵， 同时看出R(A)和R(B). 作行变换 可表示线性 由于含n− r个参数的解(6) 也可表示线性 组(3)的任一解， 从而 方程 组的方法和步骤， 程 若R(A)  R(B),(只 能R(A)  R(B)),则方程组无解。 若R(A) = R(B), 继续下一步