《线性代数》课程PPT教学课件（同济第五版）第二章 矩阵及其运算 第一节 矩阵

第二章 矩阵及其运算 第一节矩阵 定义1由m×n个数4g(i=1,2,m;j=1,2,n) 排成的m行n列的数表 411 C12 n d22 0n aml am2 称为m×n矩阵.简称m×n矩阵.记作

第二章 矩阵及其运算 第一节 矩 阵 定义1 由 个数 排成的 行 列的数表 m n m n a (i m j n) ij = 1,2,  , ; = 1,2,  , m m mn n n a a a a a a a a a       1 2 21 22 2 11 12 1 称为 矩阵.简称 mn矩阵.记作

1 a 1 A= 22 2 矩阵4的 (m,n元 mn 这m×n个数称为4的元素，简称为元 数a为于矩阵4的第行第列，称为矩阵的i,)元。 据不同需要还可记作A=Anx,=(amn=(a} 元素是实数的矩阵称为实矩阵 元素是复数的矩阵称为复矩阵 上一页不一页返回首页

(1) 1 1 2 1 2 2 2 1 1 1 2 1               = m m m n n n a a a a a a a a a A        据不同需要还可记作 ( ) ( ). ij m n A = Am n = aij = a   ( )元 矩阵 的 m n A , 这mn个数称为A的元素,简称为元. 元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵. 上一页 下一页 返回首页 数a ij为于矩阵A的第i行第j列，称为矩阵A的(i, j)元

例如 是一个2×4实矩阵； /1362i 1 B= 2 22 A1= 2 222 4 是一个3×3复矩阵 是一个3×1矩阵 C=(2359) C1=(4) 是一个1×4矩阵； 是一个1×1矩阵

        − = 9 6 4 3 1 0 3 5 A 是一个 24 实矩阵；           = 2 2 2 2 2 2 13 6 2i B 是一个 33 复矩阵           = 4 2 1 是一个 31 矩阵 C = (2 3 5 9) 是一个 14 矩阵； (4) C1 = 是一个 11 矩阵. 例如 A1

几种特殊矩阵 (1)行数与列数都等于n的矩阵A,称为n阶 方阵.也可记作An 13 6 】 例如 2 2 2 是一个3阶方阵， 22 (2)只有一行的矩阵 A=(41,a2,.,an)2 称为行矩阵（或行向量） 上一页不一页返回首页

例如           2 2 2 2 2 2 13 6 2 是一个3 阶方阵. 几种特殊矩阵 (2)只有一行的矩阵 ( , , , ), A = a1 a2  an 称为行矩阵(或行向量). (1)行数与列数都等于 n 的矩阵 A ，称为 n 阶 . 方阵.也可记作 An 上一页 下一页 返回首页

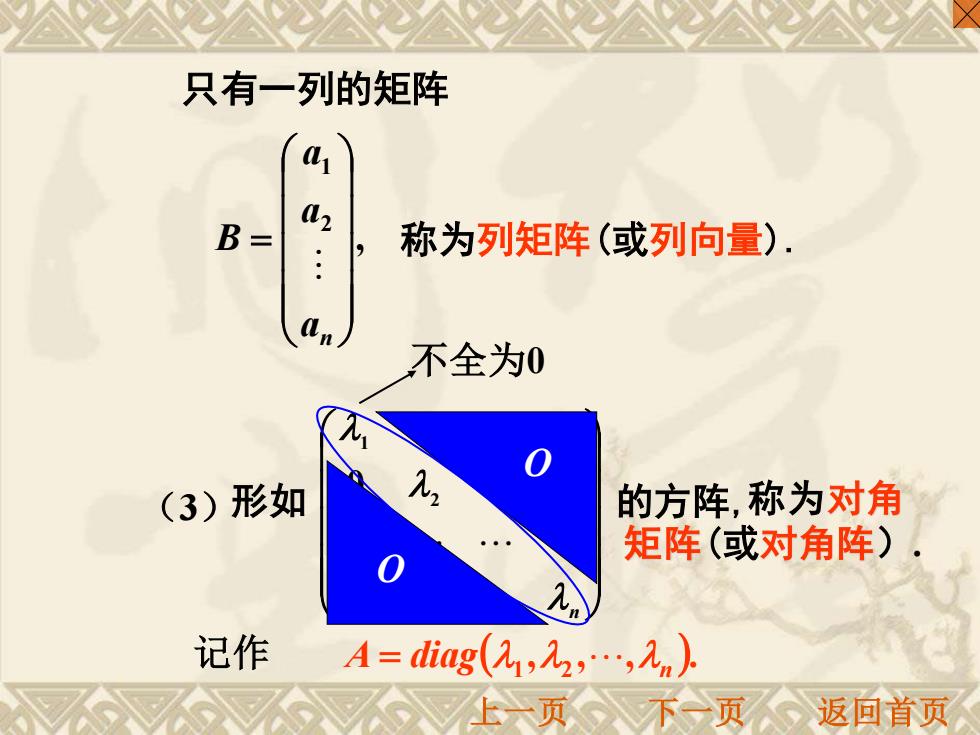
只有一列的矩阵 a B= a2 称为列矩阵（或列向量） 不全为0 (3)形如 的方阵，称为对角 矩阵（或对角阵） 记作 A=dig(,2,.,n） 上一页◇不页返回首页

, 2 1               = an a a B  只有一列的矩阵 称为列矩阵(或列向量). 称为对角 矩阵(或对角阵）.                n          0 0 0 0 0 0 2 1 （3）形如 的方阵, O O 不全为0 记作 ( , , , ). A = diag 1 2   n 上一页 下一页 返回首页