
第二节矩阵的秩 线性代教
第二节 矩阵的秩
矩阵秩的概念 定义1在m×n矩阵A中,任取k行k列 (k≤m,k≤m),位于这些行列效处的2个 元素,不改变它们在中所的位置次府得 的k阶行列式称为阵A的阶子式。 例如 A的一个二阶子式 =38, 1 23 A有一个三阶子史3-5=10. A的一个一阶子式5=-5 4
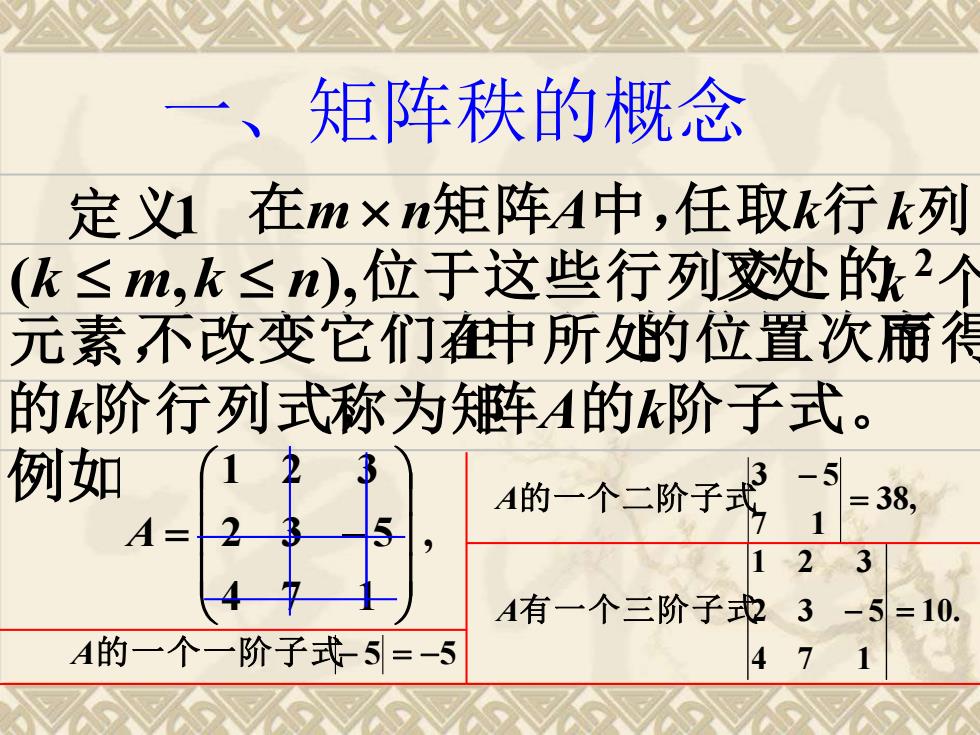
一、矩阵秩的概念 定义1 在m n矩 阵A中 ,任取k行k列 (k m,k n),位于这些行列交叉处的 元素,不改变它们在A中所处的位置次序 的k阶行列式,称为矩阵A的k阶子式。k 2 个 而得 例如 , 4 7 1 2 3 5 1 2 3 A = − A的一个一阶子式− 5 = −5 38, 7 1 3 5 = − A的一个二阶子式 10. 4 7 1 2 3 5 1 2 3 A有一个三阶子式 − =

mxn矩阵A的k阶子式共有●C东个 定义4 设在矩阵A中有一个不等的r阶子式D, 且所有r+1阶子式(如果存在酫等等, 那末D称为矩阵4的最高阶非零子式数r称为 矩阵A的秩记作R(A). 规定零矩阵的秩等研 说明①)由行列式的性质在A中当所有r+1阶 子式全等时,所衔高阶除战等铨筹d。 因此把阶非式称为最阶非零子式 m×n矩阵A的秩R(A)就是A中非零子式日 最高阶数
m n 矩 阵A的k 阶子式共有 个. k n k Cm •C 定义4 设在矩阵A中有一个不等于0的 r 阶子 式D, 且所有r + 1阶子式(如果存在的话)全等等于0, 那 末D 称为矩阵A的最高阶非零子式, 数r称为 矩阵A的秩,记作R(A). 规定零矩阵的秩等于0. 说明(1) 所有r + 2阶子式等于多少?为0. 由行列式的性质知,在 A中当所有r +1阶 子式全等于0时,所有高于r +1阶子式 最高阶数。 也全等于0, 因此把r阶非零子式称为最高阶非零子式, m n 矩 阵A的 秩R (A) 就 是A中非零子式的

说明2) 由于RA)是A的非零子式的最高阶鸯 因此,若矩阵私中有某个s阶子式不为, 则R(A)≥S; 若矩阵A中所有阶子式全, 则R(A)<t. 说明3) 若A为mx矩阵则b≤R()≤min{m,n. 说明4)对于A',其子式和4的子式对应相等 从而R(A)=R(A). 说明6) 对于n阶矩阵A,由于A的n阶子式只有一斜
对于A T ,其子式和A的子式对应相等, R(A ) R(A). T 从而 = 说明(2) 由 于R(A)是A的非零子式的最高阶数, 因此,若矩阵A中有某个s阶子式不为0, 则R(A) s; 若矩阵A中所有t阶子式全为0, 则R(A) t. 说明(3)若A为mn矩阵,则0 R(A) minm,n. 说明(4) 说明(5)对 于n阶矩阵A,由 于A的n阶子式只有一个A

故当A≠0时R(A)=n, 当A=0时R(A)<n. 可见n阶方阵4可逆台A≠0 台R(A)=n 即A的秩为n. 1 23 02 3 例如 A= 2 3-5 A=23-5=-18≠0, 7 47 1 故R(A)=n,A可逆
18 0, 4 7 1 2 3 5 0 2 3 A = − = − 故当A 0时 可见 n阶方阵A可逆 = − 4 7 1 2 3 5 1 2 3 A 故 R(A) = n, A可逆。 R(A) = n, 当 A = 0时 R(A) n. R(A) = n 即A的秩为n. A 0 例如