
第5牵相帜斑阵风二次型 第一节向量的内积,长度及正 交性
第一节 向量的内积,长度及正 交性
、 内积的定义及性质 定义1 设有n维向量 例如 XI y 2 0 X2 0= B= x= y= -2 0 令[xy]= 1y a ]=-5 称[x,y]为向量x与y的内积
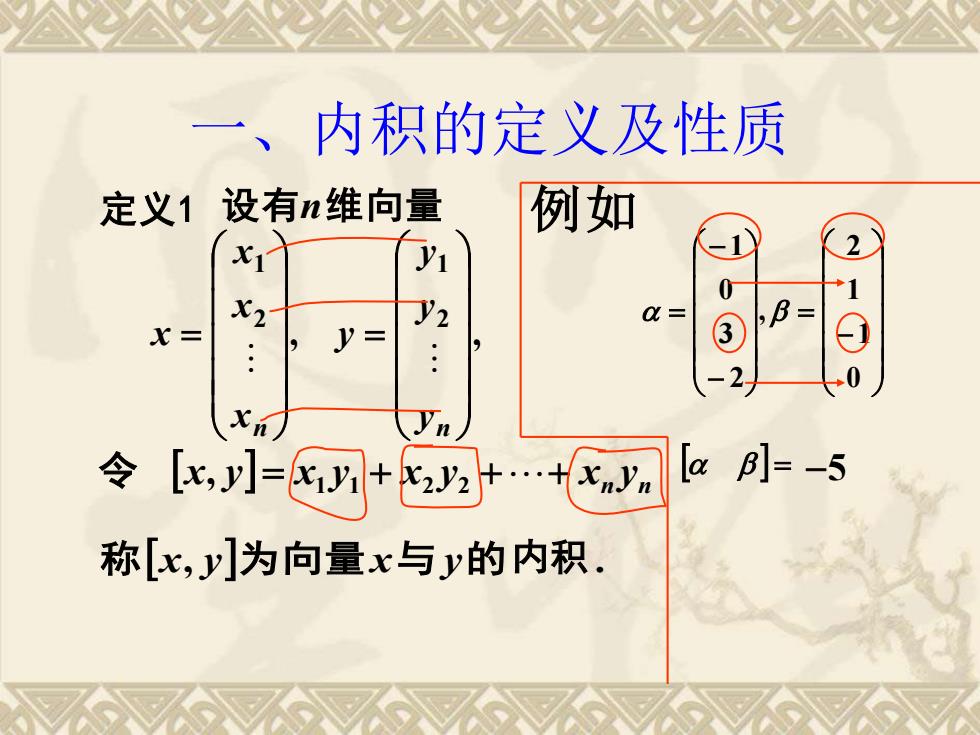
定义1 设有n维向量 , , 2 1 2 1 = = n n y y y y x x x x n n x y = x y + x y ++ x y 1 1 2 2 令 , 称x, y为向量x与 y的 内积 . 一、内积的定义及性质 例如 − = − − = 0 1 1 2 , 2 3 0 1 = −5

说明 1n(n≥4)维向量的内积是3维向量数量积 的推广,但是没有3维向量直观的几何意义. 2内积是向量的一种运算,如果x,y都是列 向量,内积可用矩阵记号表示为: [x,y]=xTy. y2 (x1,X2,Xn) =X1y1+x2y2+.+XnYn
说明 1 维向量的内积是3维向量数量积 的推广,但是没有3维向量直观的几何意义. n(n 4) , . , : 2 , , x y x y x y T = 向量 内积可用矩阵记号表示为 内积是向量的一种运算 如果 都是列 n n y y y x x x 2 1 1 2 ( , , , ) n n = x y + x y ++ x y 1 1 2 2

内积的运算性质 (其中x,y,z为n维向量,为实数): [k,]=[,x]; (2)[x,]=k,y]; (3)[x+,z]=[x,z]+[y,z] (4)[x,x≥0,且当x≠0时有[x,x>0. [xy]=x1y+x2y2++nyn
内积的运算性质 (其中x, y,z为n维向量,为实数): (1) x, y = y, x; (2) x, y = x, y; (3) x + y,z = x,z+ y,z; (4)[x, x] 0,且当x 0时有[x, x] 0. n n x y = x y + x y ++ x y 1 1 2 2

二、向量的长度及性质 定义2令 x=√x,x]=V+x++x, 称x为n维向量x的长度(或范数) 向量的长度具有下述性质: 1.非负性当x≠0时,x>0;当x=0时,x=0; 2.齐次性2x=2x; 3.三角不等式x+y川≤x+y x,y=x1y1+x2y2++xnyn
定义2 1.非负性 2.齐次性 3.三角不等式 , , 2 2 2 2 x = x x = x1 + x ++ xn 令 称 x 为n维向量x的 长度 (或 范数 ). 向量的长度具有下述性质: 当x 0时, x 0;当x = 0时, x = 0; x = x ; x + y x + y . 二、向量的长度及性质 n n x y = x y + x y ++ x y 1 1 2 2