
第三节线性方程组的解 线性代教
第三节 线性方程组的解

设有n个未知数m个方程的线性方程 0X+0,+.+0.Xn=b, 0,+0a,+.+0.Xn=b2, (3) axtax+.+ax=b 由第二章第哺知3)可以写成向量方程 Ax=b (4 今后线性方程组)与向量方程4)将混同使用而不加区 解 解向量 在名称上不加区别
设有n个未知数m个方程的线性方程 (3) , , 1 1 2 2 , 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 + + + = + + + = + + + = m m m n n m n n n n a x a x a x b a x a x a x b a x a x a x b (4) 3 Ax = b 由第二章第四节 知( )可以写成向量方程 今后线性方程组(3)与向量方程(4)将混同使用而不加区分, 解 解向量 在名称上不加区别
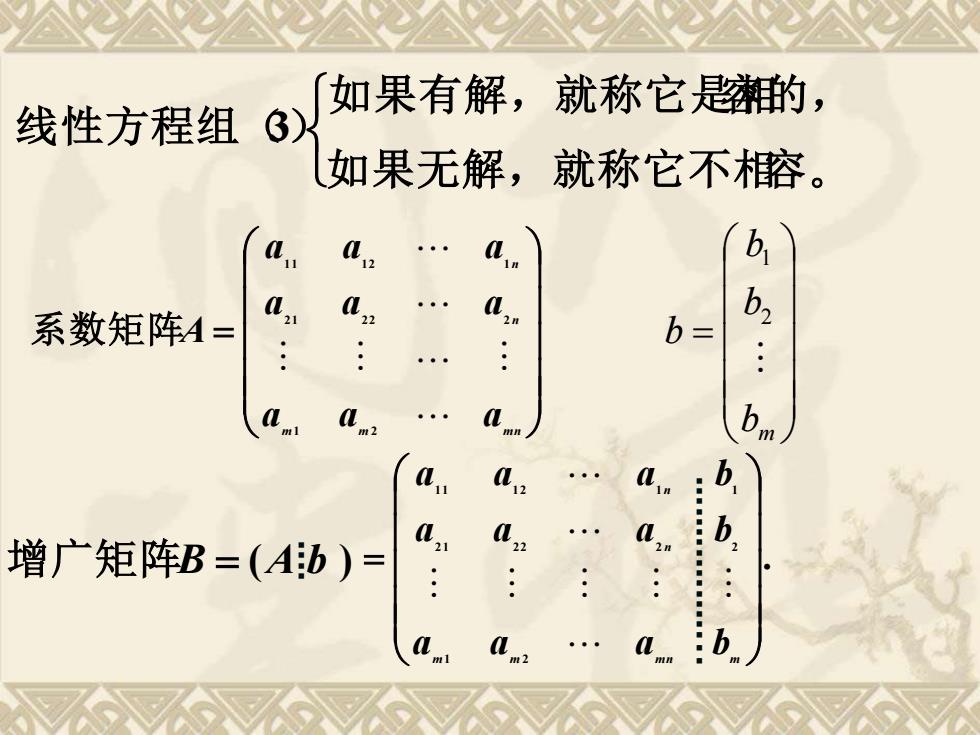
如果有解,就称它的, 线性方程组 6) 如果无解,就称它不镕。 系数矩阵A= b= b 增广矩阵B=(Ab)= N- b
如果无解,就称它不相容。 如果有解,就称它是相容的, 线性方程组(3) = m m m nnn a a a a a a a a a A 1 2 2 1 2 2 2 1 1 1 2 1 系数矩阵 = bmbb b 21 增广矩阵B = ( A b ) . 1 2 2 1 2 2 2 2 1 1 1 2 1 1 = m m m n m nn a a a b a a a b a a a b

、线性方程组有解的判定条件 问题:如何利用系数矩阵A和增广矩阵B的秩, 讨论线性方程组Ax=b的解. 定理趣n元齐次线性方程组nx=b (1)无解的充分必要条件是4)<R(B)=R(A,b): (2)有惟一解的充分必要条件是R(A=R(A,b)=n, (3)有无限多解的充分腰骅是 R()=R(A,b)<n.(n为未知数的个娄
定理3 一、线性方程组有解的判定条件 无解的充分必要条件是R(A) R(B) = R(A,b); 有无限多解的充分必要条件是 讨论线性方程组 的解. 如何利用系数矩阵 和增广矩阵 的秩, Ax b A B = 问题: ⑵ ⑴ ⑶ (n为未知数的个数) n 元齐次线性方程组Amn x = b R(A) = R(A,b) n

证明 (要证充分必要条件,必要性和充分性两 本定理只需证充分铟为 ()中条件的必要怃解→R(A)<R(A,b), (2)中条件的充分性(A)=R(A,b)=n→有惟一解 (3)中条件的充分R(A)=R(A,b)Kn→有无限解 (2),(3)两结论的逆否无解→R(A)<R(A,b) ()中条件的必要性 由此可),(3)条件中的充分性脑命题就是1) 中条件的必链同理 (2)中条件的必要是(1)3)条件的充分性櫛否命题
证明 (要证充分必要条件,需证必要性和充分性两部分 。 本定理只需证充分性, (1)中条件的必要性: (2)中条件的充分性:R(A) = R(A,b) n有无限多解, (2),(3)两结论的逆否命: (1)中条件的必要性 由此可知(2),(3)条件中的充分性的逆否命题 中条件的必要性. 无解R(A) R(A,b), (3)中条件的充分性: R(A) =R(A,b ) = n有惟一解, 因为无解R(A) R(A,b) 就是(1) 同理, (2)中条件的必要性是(1)(3) 条件的充分性的逆否命题