
3)中条件的必要恤2)条件的充分性否命题 下面我们来证此定理的分性 首先由所学内容下述结论 方程组Ar气,同解A=方(方程组 增广矩椰=(A,b)之B=(A,(增广矩阵 例如 x1+X2-3x3-x4=1, 对于方程组3x,-x2-3x3+4x4=4, x1+5x2-9x3-8x4=0
(3)中条件的必要性是(1)(2)条件的充分性的逆否命题。 下面我们来证此定理的充分性, 首先由所学内容可得下述结论: 方程组Ax = b, 增广矩阵B = (A,b) Ax = b (方程组) ~ r B = (A,b) ~ ~ ~ ~ ~ (增广矩阵) 同解 例如 + − − = − − + = + − − = 5 9 8 0. 3 3 4 4, 3 1, 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 对于方程组
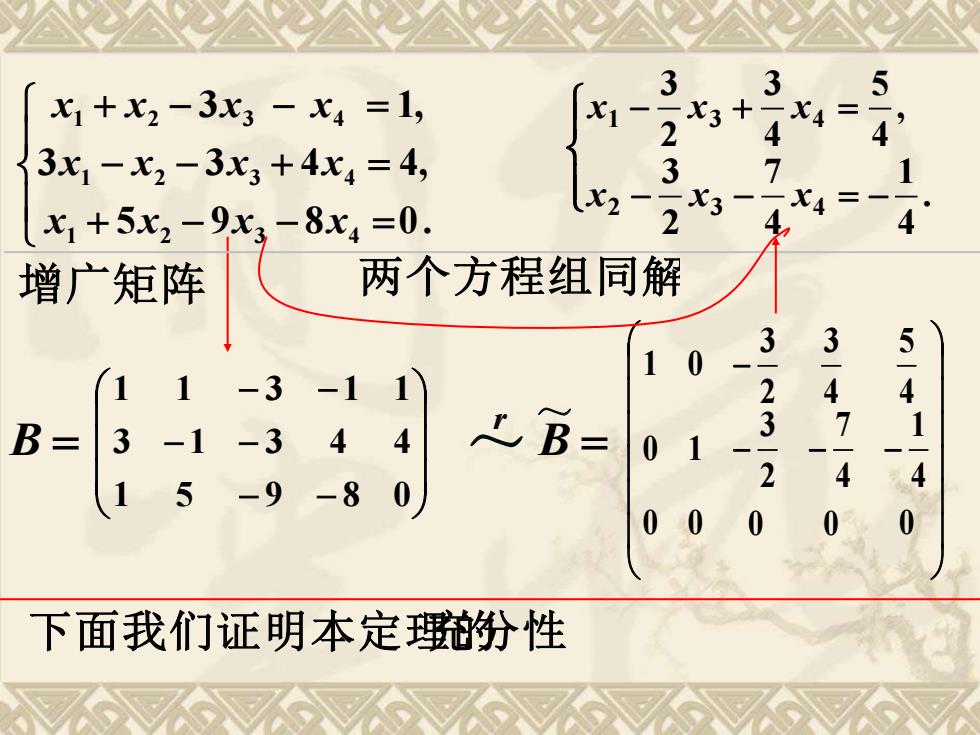
3 3 5 x1+x2-3x3-X4=1, x3+ 2 3x1-X2-3x3+4x4=4, 3 X3 2 一X4 x1+5x2-9x3-8x4=0. 4 增广矩阵 两个方程组同解 3 3 0 5 11-3-11 2 / 4 B= 3-1-3 4 人B= 3 4 01 15 2 -9 -80 00 0 下面我们证明本定理的纷性
+ − − = − − + = + − − = 5 9 8 0. 3 3 4 4, 3 1, 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 增广矩阵 B = − − − − − − 1 5 9 8 0 3 1 3 4 4 1 1 3 1 1 ~ r B = − − − − 0 0 0 0 0 4 1 4 7 2 3 0 1 4 5 4 3 2 3 1 0 ~ − − = − . 4 1 4 7 2 3 x2 x3 x4 − + = , 4 5 4 3 2 3 1 3 4 x x x 两个方程组同解 下面我们证明本定理的充分性

设R(A)=r.为叙述方便无妨设=(A,b)的行最简形 b11 bi.n-r d 0 b21 b2.n-r d B 人B= 0 b ,n-r dr 0 0 0 0 d r+1 0 0 0
设R(A) = r.为叙述方便无妨设B = (A,b)的行最简形为 + − − − 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 1 , 2 1 2, 2 1 1 1, 1 r r r n r r n r n r d b b d b b d b b d B ~ r B ~ =

看0的茹B州则B中的d+1=1, 于是B的第r+1行对应矛盾方翻=1, 故方程4)无解。 (2) 着20的充勋鹅=r=n,则B中的dr+1=0 (或d,+1不出现,且b都不出现 与B对应的方程组是 x=d, x,=d, 故方程4)有惟一解。 x.=d
⑴ 1, 则 B中的 d r + 1 = ~ 于 是B的 第 r + 1行对应矛盾方程0 = 1, ⑵ 则 B中的 d r + 1 = 0 且bij都不出现, === , 2 2 1 1 xn d n x d x d 故 方 程(4)有惟一解。 ~ ~ 若看(R1()的充分性 A) R(B), 故方程(4)无解。 ( ), 或dr+1 不出现 若看(R 2 ( )的充分性 A ) = R ( B ) = r = n , 与 B对应的方程组是 ~

(3) 藉来看承的充分性<,则B中的d =0 (或d+1不出现此时对应的方程组为 x1+b11xr+1++b1,n-rxn=1, X2+b21七r+1++b2,m-rxn=2, (⑤) xr+brxr++brn-rxn=dr2 即 x1=-b11x+1-b,n-rxn+1, x2=-b21xr+1-b2,-rxn+2, xr=-br1xr+1-brn-rxn+dr
⑶ 若R(A) = R(A) = r n, 此 时B对应的方程组为 (5) , , , 1 1 , 2 2 1 1 2, 2 1 1 1 1 1, 1 + + + = + + + = + + + = + − + − + − r r r r n r n r r n r n r n r n x b x b x d x b x b x d x b x b x d 再来看(3)的充分性 则B中的dr+1 = 0 ( ) 或dr+1 不出现 即 (6) , , , 1 1 , 2 2 1 1 2, 2 1 1 1 1 1, 1 = − − − + = − − − + = − − − + + − + − + − r r r r n r n r r n r n r n r n x b x b x d x b x b x d x b x b x d ~