《线性代数》课程PPT教学课件（同济第五版）第四章 向量组的线性相关性 第四节 线性方程组解的结构

第四节线性方程组解的结构 美学释夜

第四节 线性方程组解的结构

对于线性方程生 齐次 非齐次 411X1+412x2+.+41nXn=0 11比1+012X2+.+41mXn=b1 21X1+422X2+.+02mXn=0 a21X1+a22X2+.+2mxn=b2 0m1X1+m2X2+.+mmXn=0 +am2x2++amn xn bm 我们可以用矩阵的初换求解它们，并有的两个定理， 有非零解系数矩阵的秩 有解台R(A=RB R(A<n. 当(A)=R(B)<n时精无限多 下面我们用向量组线联的锂论来论线划耀组萌解解 先讨论齐次线性方程

对于线性方程组 齐次        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x            + + + = + + + = + + + = m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 21 1 22 2 2 2 11 1 12 2 1 1 非齐次 我们可以用矩阵的初等变换求解它们，并有如下的两个定理， 有非零解系数矩阵的秩 R(A) 有解  n. R(A) = R(B), 当R(A) = R(B)  n时 当R(A) = R(B) = n时有惟一解。 有无限多解， 下面我们用向量组线性相关的理论来讨论线性方程组的解。 先讨论齐次线性方程组

一、齐次线性方程组解的性质 1.解向量的概念 设有齐次线性方程组 4111+012X2+.+41mXn=0 L21七1+22X2++42mXn=0 (1) m1七1+0m2X2+.+mmXn=0 若记

１．解向量的概念 设有齐次线性方程组        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     若记 （1） 一、齐次线性方程组解的性质

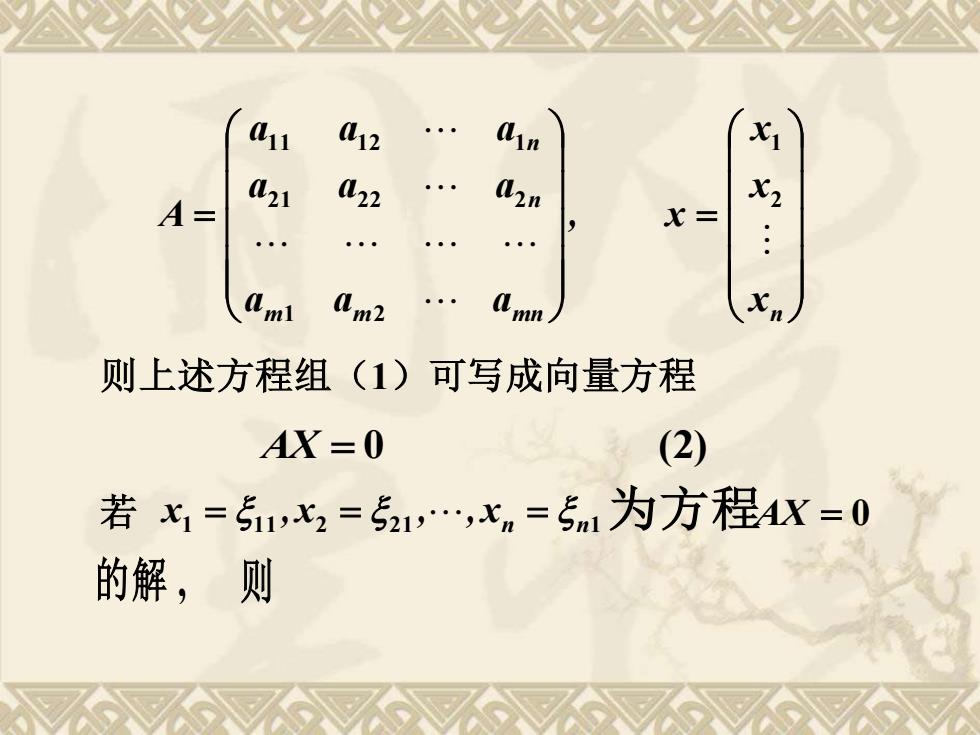
1 2 n X1 21 x2 A= l22 Q2n X= Ami (m2 mn 则上述方程组(1)可写成向量方程 AX=0 (2) 若七=1，x=521,水n=5n1为方程4X=0 的解，则

, a a a a a a a a a A m m mn n n               =        1 2 2 1 2 2 2 1 1 1 2 1               = xn x x x  2 1 则上述方程组（1）可写成向量方程 AX = 0 (2) 1 1 1 2 2 1 xn n1 若 x =  , x =  ,, =  为方程AX = 0 的解 , 则

线性方程组) 0111+012X2+.+41mXn=0 x=51= 521 21K1+22X2++42mXn=0 m火+0m2X2+.+amXn=0 称为方程组(1) 的解向量， 向量方程(2) 它也就是向量方程(2) AX=0, 的解

              = = 1 21 11 1 n x      称为方程组(1)        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     线性方程组(1) 的解向量， 它也就是向量方程(2) 的解． 向量方程(2) AX = 0