
2 3 例1求矩阵A= 23-5 的秩 471 解 在中, 又·A的3阶子式只有一个A,且A=0, ∴.R(A=2
例 1 . 4 7 1 2 3 5 1 2 3 求矩阵 的秩 A = − 解 在 A中, 又 A 的 3阶子式只有一个 A, 0. 2 3 1 2 且 A = 0 , R ( A ) = 2
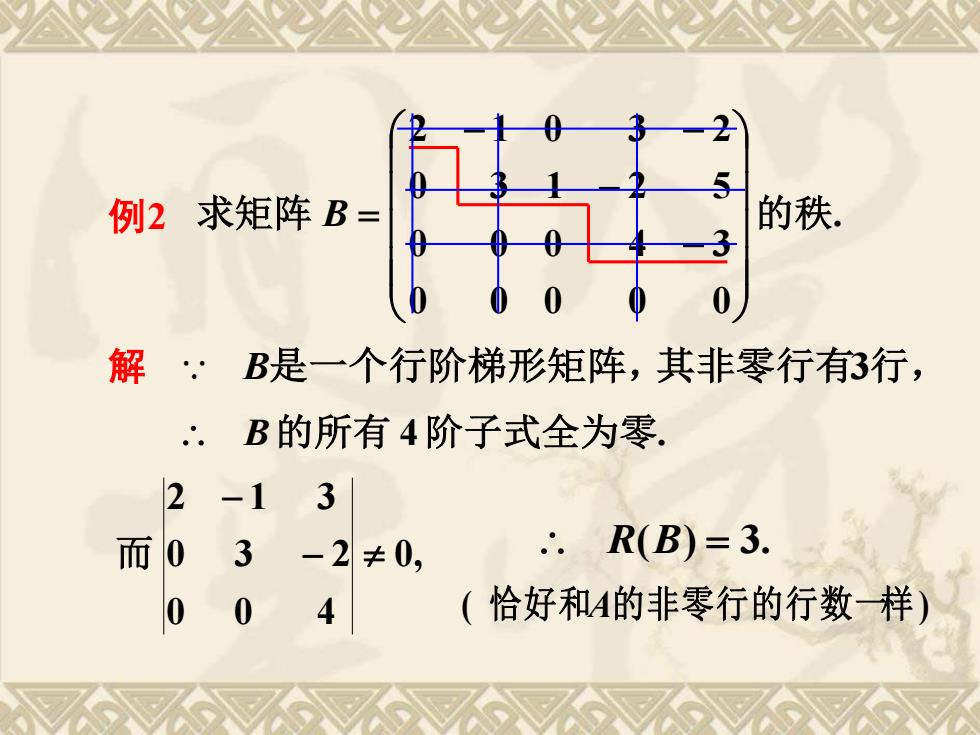
例2求矩阵B= 的秩。 解.·B是一个行阶梯形矩阵,其非零行有3行, :.B的所有4阶子式全为零. 2-13 而03-2≠0, .R(B)=3. 0 0 4 (恰好和A的非零行的行数样
例 2 . 0 0 0 0 0 0 0 0 4 3 0 3 1 2 5 2 1 0 3 2 求矩阵 的秩 − − − − B = 解 B是一个行阶梯形矩阵,其非零行有3行, B的所有 4阶子式全为零. 0, 0 0 4 0 3 2 2 1 3− − 而 R(B) = 3. ( 恰好和A的非零行的行数一样)

例3 已知A= 求该矩阵的秩, 13 解 02 =2≠0,计算A的3阶子式, 1 3 -2 1323-2 2 -2 2 0 2 -1=0023≡0,-1 3≡00 -1 3=0, -20 1-2 05015-2 15 =0. ∴.R(A)=2
例3 已知 ,求该矩阵的秩. − − − = 2 0 1 5 0 2 1 3 1 3 2 2 A 2 0, 0 2 1 3 = 2 0 1 0 2 1 1 3 2 − − − 2 0 5 0 2 3 1 3 2 − 解 计算A的3阶子式, = 0, = 0, 0 1 5 2 1 3 3 2 2 − − 2 1 5 0 1 3 1 2 2 − − − = = 0, = 0, = = = 0. R(A) = 2

二、矩阵秩的求法 从以上三例可知,对般的矩铛行数和列数较高册 用定义求秩是很麻烦的算很多行列想从我们也看至 对行阶梯形矩咤秩就等于非霉的数一看便知毋须计 因此就想到把要求的阵与行阶梯矩阵来从我们所学 内容可知任何非零轲用初等变换化梯矩等价 问题是这两个等价的秩相等吗?看定理: 定理2若A~B,则R(A)=R(B). 先证明:若4经一次初等行变换变的 则R(A)≤R(B). 设R(A)=r,且A的某个r阶子式D,≠0
二 、矩阵秩的求法 从以上三例可知,对于一般的矩阵,当行数和列数较高时, 用定义求秩是很麻烦的(计算很多行列式)。但从例2我们也看到 对于行阶梯形矩阵,它秩就等于非零行的行数,一看便知毋须计算。 因此就想到把要求秩的矩阵与行阶梯矩阵联系起来,从我们所学 内容可知任何非零矩阵均可用初等变换化为行阶梯矩阵,(等价) 问题是这两个等价的矩阵的秩相等吗?看下面的定理: 定理2 若A ~ B, 则R(A) = R(B). 先证明:若A经一次初等行变换变为B, 设R(A) = r, 则R(A) R(B). 0. Dr 且A的某个r 阶子式

当AB或AxB时, 在B中总能找到与D,相对应的子式D,· 由于D,=D.或D,=-Dn或D,=kD, 因此D≠0,从而R(B)≥. 当AB时,分三种情况讨论 ①D中不含第i行; (2) D中同时含第i行和第i行; (3) D中含第i行但不含第i行; 上一页G入不页返首页
当A B或A B时 , 当A B时,分三种情况讨论:r ,. 在 B 中总能找到与 Dr 相对应的子式 D , r r r r r 由于 Dr = D 或 D = −D 或 D = kD D 0 R(B) r. 因此 r ,从而 () 中含第 行但不含第 行; () 中同时含第 行和第 行; () 中不含第 行; D i j D i j D i r r r 3 2 1 上一页 下一页 返回首页 ~ i j ~ r r ri k ~ i krj r +