向量代数与空间解析几何 1.椭球面 x2 22 a2 b2 c2=1(ab,c为正数) Z (1)范围: Ixl≤alyl≤b,lzl≤c (2)与坐标面的交线:椭圆 ,z2 22 c2 1 y=0
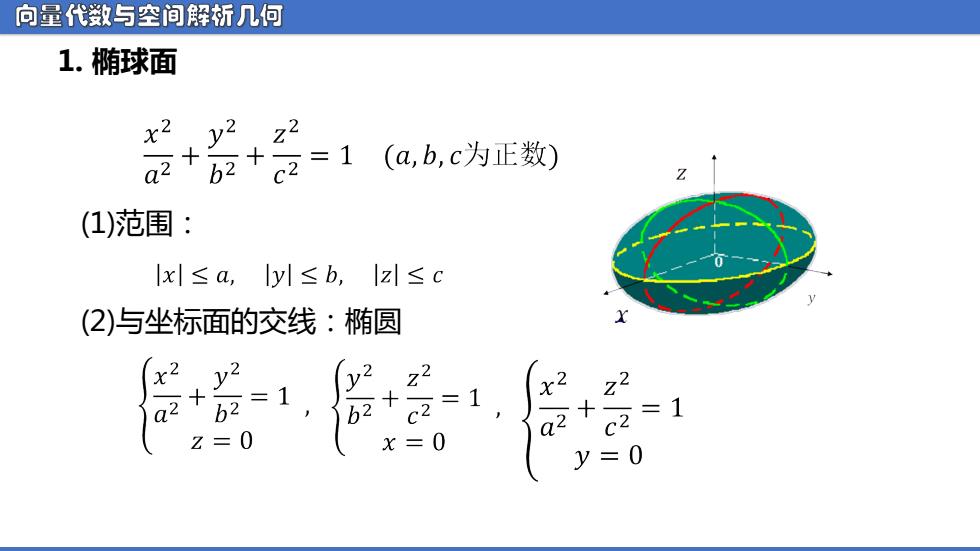
向量代数与空间解析几何 1. 椭球面 (1)范围: (2)与坐标面的交线:椭圆

向量代数与空间释析几何 x2,y2 2 2+ 2+c2 =1 (abc ,为正数) (3)截痕:与z=z1(z1<c)的交线为椭圆: x2 y2 ce-)e2-z =1 之=2, 同样x=x1(x1|≤a)及y=y1(ly1|≤b) 的截痕也为椭圆! (4)当α=b时为旋转椭球面;
向量代数与空间解析几何 与 的交线为椭圆: ᵆ = ᵆ 1 的截痕也为椭圆. (3) 截痕: (ᵄ ,ᵄ ,ᵅ 为正数)