《线性代数》课程PPT教学课件（同济第五版）第三章 矩阵的初等变换与线性方程组 第一节 矩阵的初等变换

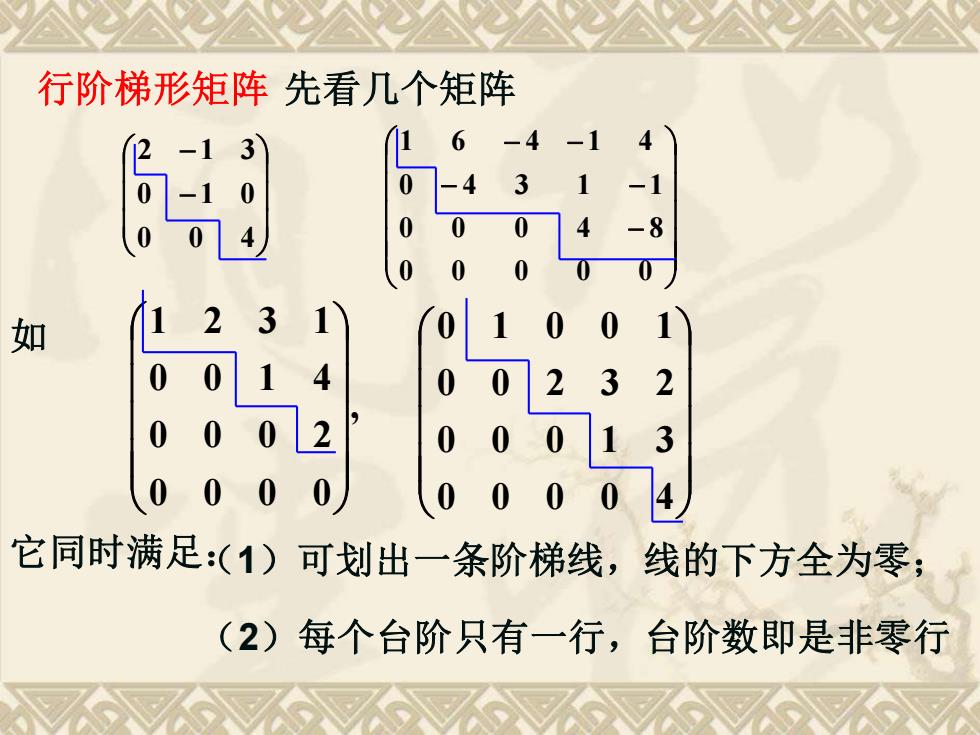
行阶梯形矩阵先看几个矩阵 -4 0 0 如 3 0 0 0 0 0 它同时满足：()可划出一条阶梯线， 线的下方全为零； (2)每个台阶只有一行，台阶数即是非零行

行阶梯形矩阵 先看几个矩阵           − − 0 0 4 0 1 0 2 1 3               − − − − − 0 0 0 0 0 0 0 0 4 8 0 4 3 1 1 1 6 4 1 4 , 0 0 0 0 0 0 0 2 0 0 1 4 1 2 3 1                             0 0 0 0 4 0 0 0 1 3 0 0 2 3 2 如 0 1 0 0 1 它同时满足：（1）可划出一条阶梯线，线的下方全为零； （2）每个台阶只有一行，台阶数即是非零行

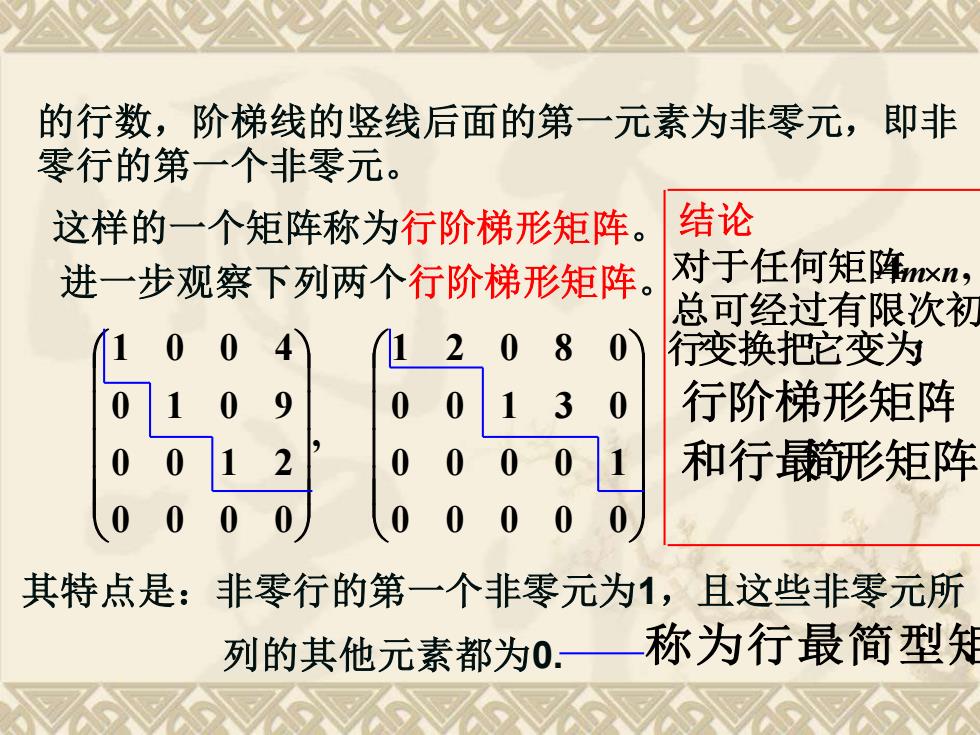
的行数，阶梯线的竖线后面的第一元素为非零元，即非 零行的第一个非零元。 这样的一个矩阵称为行阶梯形矩阵。 结论 进一步观察下列两个行阶梯形矩阵。 对于任何矩阵xn, 总可经过有限次初 1 0 12 0 8 行变换把它变为 071 0 9 0( 3 行阶梯形矩阵 00 12i 0 000 和行最形矩阵 0 00 其特点是：非零行的第一个非零元为1，且这些非零元所 列的其他元素都为0.— 称为行最简型

的行数，阶梯线的竖线后面的第一元素为非零元，即非 零行的第一个非零元。 这样的一个矩阵称为行阶梯形矩阵。 进一步观察下列两个行阶梯形矩阵。 , 0 0 0 0 0 0 1 2 0 1 0 9 1 0 0 4                             0 0 0 0 0 0 0 0 0 1 0 0 1 3 0 1 2 0 8 0 其特点是：非零行的第一个非零元为1，且这些非零元所 列的其他元素都为0. 结论 对于任何矩阵Amn, 总可经过有限次初等 行变换把它变为: 行阶梯形矩阵 和行最简形矩阵。 称为行最简型矩阵

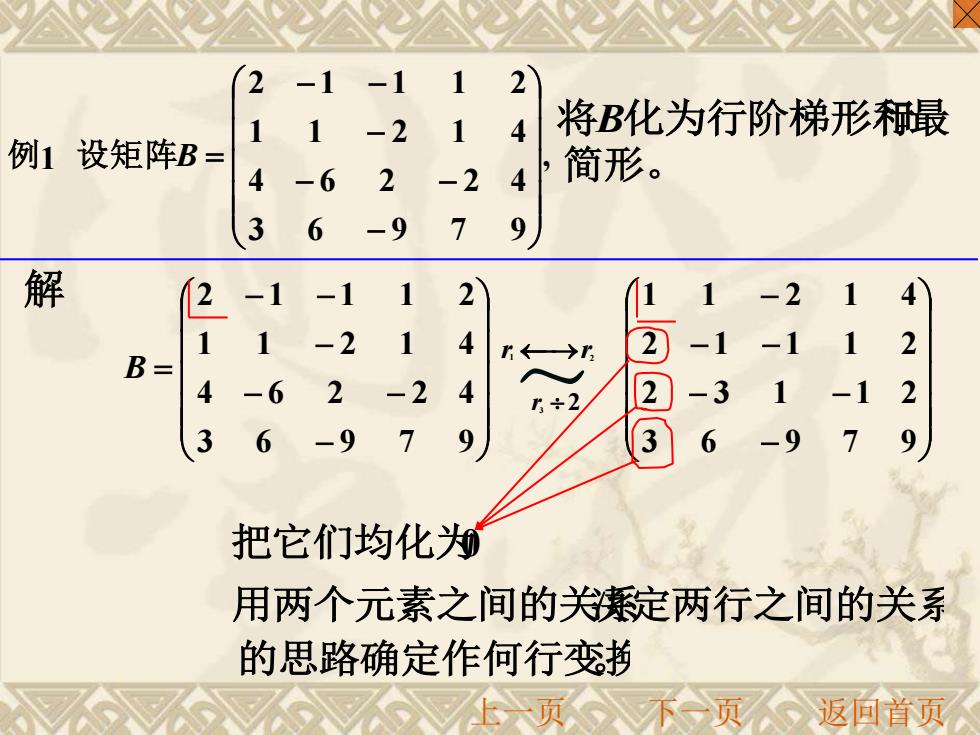
2 -1 1 2 1 4 将B化为行阶梯形最 例1设矩阵B= 4 -6 2 -2 4 简形。 3 6 -9 7 9 解 2 -1 -1 1 2 1 -214 1 -2 1 4 B= 2 -1 -1 1 2 4-6 2 -2 5÷2 -3 1 -1 2 3 6 -9 3 6 -9 7 9 把它们均化 用两个元素之间的关定两行之间的关系 的思路确定作何行变 上一页入不页返向首页

上一页 下一页 返回首页 , 3 6 9 7 9 4 6 2 2 4 1 1 2 1 4 2 1 1 1 2 1               − − − − − − 例 设矩阵B = 将B化为行阶梯形和行最 简形。 解               − − − − − − = 3 6 9 7 9 4 6 2 2 4 1 1 2 1 4 2 1 1 1 2 B ～ r1 ⎯→r2               − − − − − − 3 6 9 7 9 2 3 1 1 2 2 1 1 1 2 1 1 2 1 4 r3  2 把它们均化为0 用两个元素之间的关系决定两行之间的关系 的思路确定作何行变换

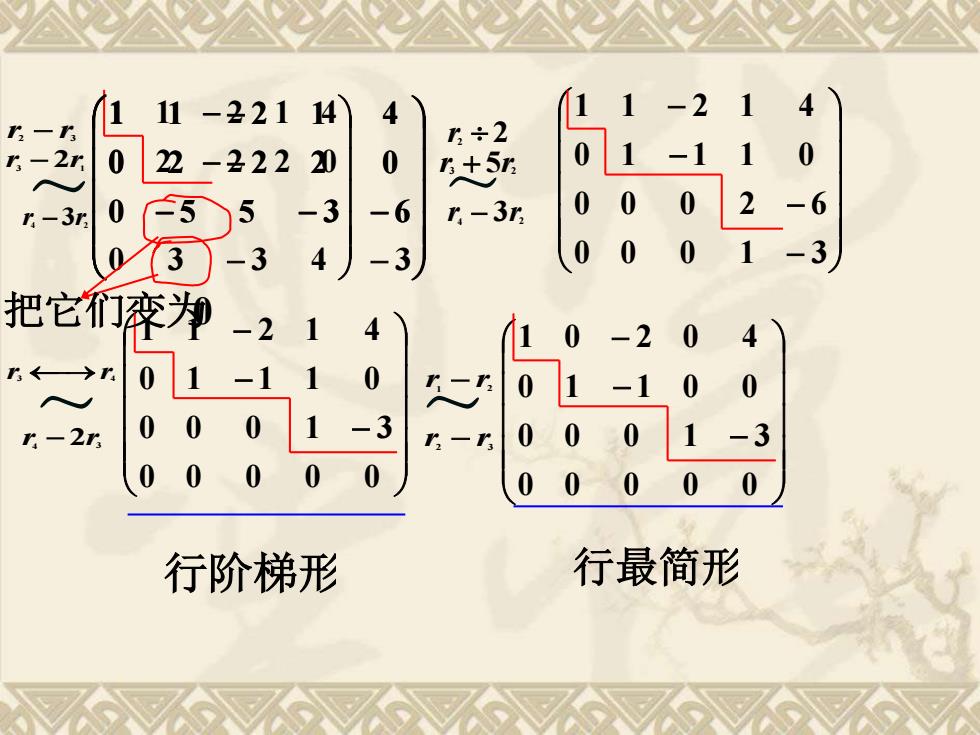
11-221 14 4 ÷2 0 2-222 20 0 +5r 1-20 01 n.-3n 0 5 -3 -6 r-3 00 0T3 -3 4 -3 0 0 把它们瘠押 -2 1 4 1 0 -2 01 -1 0 二 0 1 -1 0 r-2r 00 0 -3 00 0 -3 0 0 0 0 00 0 0 0 行阶梯形 行最简形

r2 − r3 r2  2 r4 − 3r2               − − − − − − − 0 3 3 4 3 0 5 5 3 6 0 2 2 2 0 1 1 2 1 4 ～ r3 − 2r1 ～ r3 + 5r2 r4 − 3r2               − − − − 0 0 0 1 3 0 0 0 2 6 0 1 1 1 0 1 1 2 1 4 ～ r3 ⎯→r4 r4 − 2r3               − − − 0 0 0 0 0 0 0 0 1 3 0 1 1 1 0 1 1 2 1 4 ～ r1 − r2 r2 − r3               − − − 0 0 0 0 0 0 0 0 1 3 0 1 1 0 0 1 0 2 0 4 行阶梯形 行最简形               − − 0 2 2 2 0 1 1 2 1 4               − − − − − 0 5 5 3 6 0 2 2 2 0 1 1 2 1 4 把它们变为0