X1=-611xr+1-b1,n-rxn) xr=-br1xr+1-brn-rxn 七+1,x+1,.,xn作自由未知数, 并令x,+1=G1,水,+2=C2,xn=Cn-,可得方程组1) 的通解如下x -b11 -b12 -bi Xr -ba br2 Xr+l =C1 1 十C2 0 1 X+2 0 1 0 Xn 0 0 0
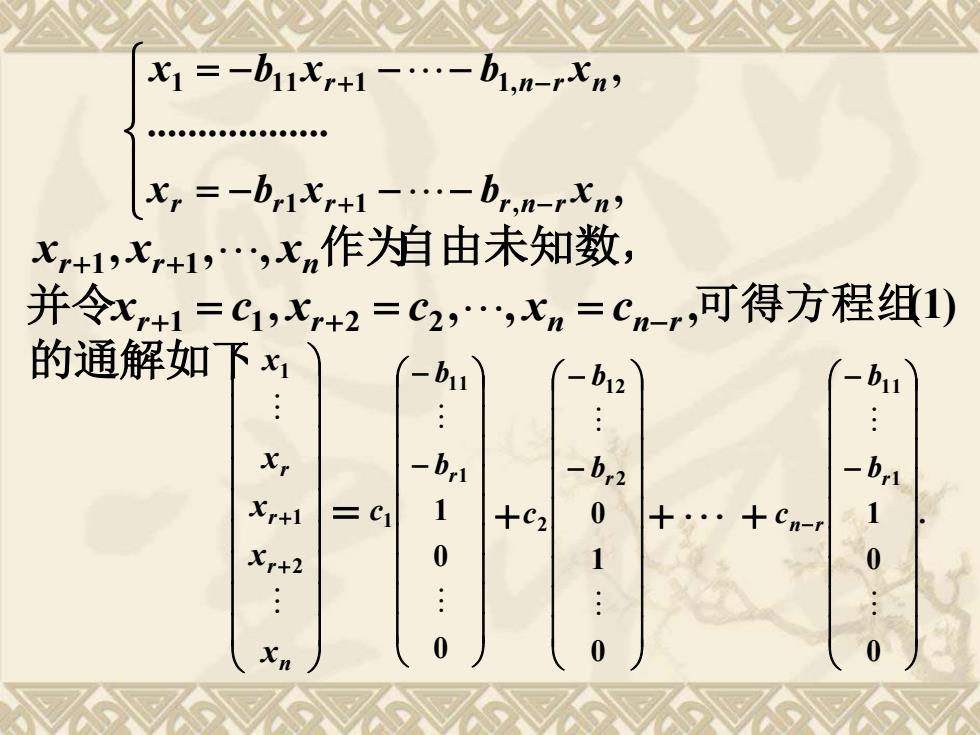
= − − − = − − − + − + − , . , 1 1 , 1 1 1 1 1, r r r r n r n r n r n x b x b x x b x b x = 自由未知数, , , , , r 1 1 r 2 2 n n r x c x c x c 并令 + = + = = − 可得方程组(1) + + + n r r r x x x x x 2 1 的通解如下 1 xr+1 , xr+1 , , xn 作为 − − 0 0 1 1 11 1 r b b c − − 0 1 0 2 12 2 r b b c . 0 0 1 1 11 − − − r n r b b + + c

把上式记作 x=G151+C252++Cm-,5m-r, 由此可知解集中的任一向量能由5,专m 线性表方 另一方面在矩阵 (-b11-b12.-b,m-r -br -b r,n-r (51,52,5m-)= 1 0 0 0 1 0 : 0
把上式记作 , 1 1 2 2 n r n r x c c c = + ++ − − 由此可知解集S中的任一向量x能由 1 ,, n−r 线性表示, 另一方面在矩阵 ( , , , ) 1 2 n−r = − − − − − − − − 0 0 1 0 1 0 1 0 0 1 2 , 1 1 1 2 1, r r r n r n r b b b b b b

中有一个n-阶子式En,≠0,由矩阵秩的定义可有 R(51,52,.,5m-r)=n-r, 故51,5m,线性无关。总上可知 (1)5,5m,线性无关。 (2)解集中的任一向量能由51,5m,线性表示。 根据最大无关组的等鎚义可1,5m-是解集S的 最大无关组即51,5m-,就是方程组1)的基础解系 如何求出基解彩,5m-,呢我们回去看看如何得 ,5m-,的,这是我们求基础解系越本方法之
− 0, En−r 中有一个n r阶子式 ( , , , ) , 1 2 R n r n−r = − 由矩阵秩的定义可得 是解集S的 最大无关组。 n−r , 故 1 , 线性无关。总上可知 (1) 1 , , n−r 线性无关。 (2)解 集S中的任一向量x能由 1 ,, n−r 线性表示。 根据最大无关组的等价定义可知 1 ,, n−r 即 1 ,, n−r 就是方程组(1)的基础解系。 如何求出基础解系 1 ,, n−r 呢? 1 ,, n−r 的, 我们回去看看如何得到 这是我们求基础解系的基本方法之一

我们还可以用其它基础解翼体的作法我们 在后面的例子中详细绮。 现在我们依据上面求解紊1,.,5m-,的讨论还可 得出下面重要的定理 定理7设m×n矩阵A的秩R()=r,则n元齐次线性 方程组Ar=O的解集S的秩R。=n一r. 说明(L)当R(A)=r=n时,R。=0,此时解集S只含 一个零向纵而方程细)只有零解股有基解系 (2)当R(A)=r<时由定理7可知方程组1)的基础角 系含n-个向量。方程组的任何1-r个线性无 的解都可构成它的基础解蹇础解系和通解雁
我们还可以用其它方法求基础解系, 1 ,, n−r 具体的作法我们会 在后面的例子中详细介绍。 现在我们依据上面求基础解系 的讨论,还可 得出下面重要的定理 设m n矩 阵A的 秩R(A) = r,则n元齐次线性 (1)当R(A) = r = n时 , 定理7 方程组Ax = 0的解集S的秩R n r. s = − = 0, 说明 Rs 方程组(1) 此时解集S只含 一个零向量, (2)当R(A) = r n时, 从而方程组(1)只有零解, 由定理7可知 的基础解 系含n − r个向量。方程组(1)的任何n− r个线性无关 没有基础解系; 的解都可构成它的基础解系。基础解系和通解不惟一

下我们烈竣盟耀堃程组的基础解解 X1+x2-x3-4=0, 2x1-5x2+3x3+2x4=0, 7x1-7x2+3x3+x4=0 的基础解系与通解. 解法一对系数矩阵A作初等行变换,变为行最简矩阵, /11 -1 -1 0-2/7-3/7 A= 2-5 3 -5/7-4/7 7-7 8 0
例12 求齐次线性方程组 − + + = − + + = + − − = 7 7 3 0 2 5 3 2 0, 0, 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 的基础解系与通解. 解法一 − − − − = 7 7 3 1 2 5 3 2 1 1 1 1 A 对系数矩阵 作初等行变换, 下面我们举例说明如何求方程组的基础解系和通解。 A 变为行最简矩阵, , 0 0 0 0 0 1 5 7 4 7 1 0 2 7 3 7 − − − − r ~