
定积分 注:若不做代换,就不换限 ge=eia号=-e 0=1- 例5求?sin4 xcosxdx 解:sin4 xcosxdx=sin4 xdsinx sin5x 1 5 2= 0
定积分 注:若不做代换,就不换限

定积分 例4* 求 「2 x2 dx 0V1-x2 解: 设x=sint,则dx=costdt 当x=0时t =0 x=2 时t=名 代入原式得: 1 "2 x2 6 dx= sin2tdt 61-c0S2t dt V1-x2 Jo 2 1π1 π1 3 -2sin2t 6) 0 12 8
定积分 例4* 求 代入原式得:

定积分 例5设f(x)在[-a,a上连续,试证明 .e x为偶数, x为奇数. 证:因为 ∫"F)dix=∫fea+0fea (1) 对积分∫°nf(x)dx做变量代换x=-t, 得心rwax=-f-e业=r-a
定积分 上连续,试证明 证: 因为 得 (1)
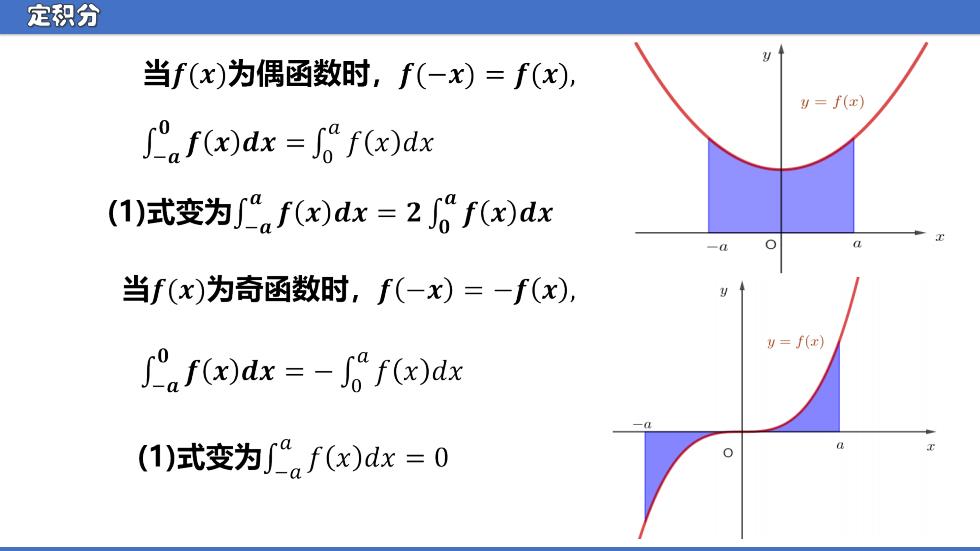
定积分 当f(x)为偶函数时,f(-x)=f(x), y=f(x) ∫afx)dx=f(x)dx (1)式变为af(x)dx=2f(x)dx 当f(x)为奇函数时,f(-x)=-f(x), y=f(x) ∫afx)dx=-fx)dx (1)式变为∫.f(x)dx=0 a 2
定积分